wektor

wektor

[łac.],

mat. uporządkowana para punktów, z których jeden, np. P(x₁, y₁, z₁), stanowi początek wektora, a drugi, np. Q(x₂, y₂, z₂) — jego koniec, przy czym x₁, y₁, z₁ oraz x₂, y₂, z₂ są współrzędnymi kartezjańskimi punktów P i Q;

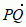prosta łącząca punkty P i Q określa kierunek wektora, a ich porządek — zwrot wektora; długość odcinka PQ stanowi długość wektora (przy obranej jednostce długości); wektor oznacza się symbolami lub , zaś jego długość symbolami ||, |  |, 2 wektory i  są równe, jeżeli leżą na prostych równoległych, mają ten sam zwrot i tę samą długość; wszystkie wektory w przestrzeni 2-wymiarowej (tzn. na płaszczyźnie) lub w przestrzeni 3-wymiarowej (a także w n-wymiarowej), które są równe, stanowią klasę zwaną wektorem swobodnym; tak więc mówiąc o wektorze bez podania jego początku (punktu zaczepienia), mówi się o całej klasie wektorów; początkiem takiego wektora można przyjąć w dowolnym punkcie (równoległe przesunięcie wektora); wektorem zerowym nazywa się wektor o długości równej 0. Na wektorach można wykonywać rozmaite działania, otrzymując w wyniku liczby lub nowe wektory; zagadnienia te są domeną rachunku wektorowego; termin wektor wprowadził w połowie XIX w. W.R. Hamilton.