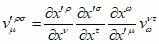wielkość, która przy zmianie układu współrz. przekształca się w specyficzny dla niej sposób; jeśli w układzie współrz. (α), współrz. punktu P są liczby x1, x2, ... , xn, to przy przejściu do nowego układu (α′) współrz. tego samego punktu będą x′1, x′2, ... , x′ n; te nowe — primowane współrz. można wyrazić jako funkcje starych w postaci równań:
x′μ = x′μ(x1, x2, ... , xn) (μ = 1, 2, ... , n), (∗)
które stanowią przekształcenie (transformację) współrz. (
α)
→ (
α′), przy czym zakłada się, że funkcje te są ciągłe, różniczkowalne i wzajemnie jednoznaczne. Jeżeli dla każdego układu współrz. (
α) jest określona funkcja punktu
φ (
x1, ... ,
xn) tak, że dla układu primowanego (
α′) jest
φ′ (
x′
1, ... ,
x′
n), i jeżeli przy przejściu od układu (
α) do układu (
α′) wartości tych funkcji
φ i
φ′ w odpowiednich punktach
xμ i
x′
μ są równe, tj. jeżeli
φ(
x1, ... ,
xn) =
φ′ (
x′
1, ... ,
x′
n), to taką funkcję punktu
φ nazywa się
skalarem (dokładniej —
polem skalarnym) lub
niezmiennikiem (oznaczenie: inv).
Wektorem kontrawariantnym nazywa się wielkość
vμ (wskaźnik
μ u góry, na pozycji kontrawariantnej), której składowe (współrz.)
v1,
v2, ... ,
vn przy przekształceniu układu współrz. (
α) → (
α′) przekształcają się (transformują się) zgodnie ze wzorami:
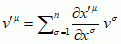
(lub
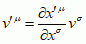
) (∗∗)
(znak sumowania Σ często pomija się zgodnie z tzw.
konwencją Einsteina, wg której znak Σ można pominąć, gdy wskaźnik sumacyjny, w tym wypadku
σ, występuje dwukrotnie — raz u góry i raz u dołu); analogicznie, jeżeli zespół wielkości
v1,... ,
vn podlega regule transformacyjnej:
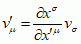
(∗∗∗)
to zespół ten określa
wektor kowariantny vμ (wskaźnik
μ u dołu, tj. na pozycji kowariantnej) o składowych
v1, ... ,
vn; skalar nazywa się też tensorem rzędu zerowego, a wektor (kontra- lub kowariantny) — tensorem rzędu pierwszego. W rachunku tensorowym rozważa się też tensory wyższych rzędów (np. drugiego o
n2 składowych, trzeciego o
n3 składowych), mające więcej niż 1 składnik; jeżeli tensor ma tylko wskaźniki górne, nazywa się t.
kontrawariantnym, jeśli tylko dolne —
t. kowariantnym, a jeżeli ma wskaźniki i górne, i dolne — tensorem
mieszanym; ogólnie tensor rzędu (
p +
q), oznaczany symbolem
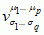
(
μ,
σ przebiegają wartości 1, 2, ... ,
n) ma
np + q składowych i (
p +
q) wskaźników; parę liczb (
p,
q) nazywa się
walencją tensora — przy przekształceniu (∗) składowe kontrawariantne tensora (numerowane górnymi wskaźnikami) transformują się zgodnie ze wzorami (∗∗) — a składowe kowariantne tensora (numerowane dolnymi wskaźnikami) — zgodnie z wzorami (∗∗∗), np. tensor trzeciego rzędu o walencji (2,1) podlega regule transformacyjnej:
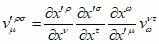
(sumowanie względem
ν,
τ i
ω od 1 do
n); tensor
v...μ...ρ nazywa się symetrycznym względem wskaźników
μ i
ρ, jeżeli
v...μ...ρ =
v...ρ...μ, zaś antysymetrycznym (lub skośnie symetrycznym), gdy
v...μ...ρ = −
v...ρ...μ; właściwościami tensorów zajmuje się
rachunek tensorowy.
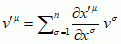 (lub
(lub 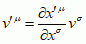 ) (∗∗)
) (∗∗) 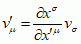 (∗∗∗)
(∗∗∗) 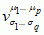 (μ, σ przebiegają wartości 1, 2, ... , n) ma np + q składowych i (p + q) wskaźników; parę liczb (p, q) nazywa się walencją tensora — przy przekształceniu (∗) składowe kontrawariantne tensora (numerowane górnymi wskaźnikami) transformują się zgodnie ze wzorami (∗∗) — a składowe kowariantne tensora (numerowane dolnymi wskaźnikami) — zgodnie z wzorami (∗∗∗), np. tensor trzeciego rzędu o walencji (2,1) podlega regule transformacyjnej:
(μ, σ przebiegają wartości 1, 2, ... , n) ma np + q składowych i (p + q) wskaźników; parę liczb (p, q) nazywa się walencją tensora — przy przekształceniu (∗) składowe kontrawariantne tensora (numerowane górnymi wskaźnikami) transformują się zgodnie ze wzorami (∗∗) — a składowe kowariantne tensora (numerowane dolnymi wskaźnikami) — zgodnie z wzorami (∗∗∗), np. tensor trzeciego rzędu o walencji (2,1) podlega regule transformacyjnej: