forma różniczkowa, forma zewnętrzna,
mat. antysymetryczne, kowariantne pole tensorowe (tensor) rzędu p (f.r. stopnia p); równoważnie: gładki przekrój p-tej potęgi zewnętrznej wiązki kostycznej (tzn. wiązki funkcjonałów liniowych na wiązce stycznej) do danej rozmaitości;
forma różniczkowa
Encyklopedia PWN
w lokalnym układzie współrzędnych x = (x1, ... , xn) na rozmaitości n-wymiarowej M (np. na przestrzeni ℝn) każda f.r. stopnia p zapisuje się jako 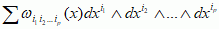 , gdzie sumowanie rozciąga się na wszystkie układy indeksów 1≤ i1 < i2 < ... < ip ≤ n; zbiór wszystkich f.r. stopnia p na rozmaitości M oznacza się symbolem Ωp(M); tzw. kompleks de Rhama
, gdzie sumowanie rozciąga się na wszystkie układy indeksów 1≤ i1 < i2 < ... < ip ≤ n; zbiór wszystkich f.r. stopnia p na rozmaitości M oznacza się symbolem Ωp(M); tzw. kompleks de Rhama 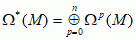 i związane z nim grupy kohomologii de Rhama odgrywają ważną rolę w geometrii różniczkowej i topologii algebraicznej; dzięki wprowadzeniu języka f.r. różne wzory całkowe analizy wektorowej, będące uogólnieniami podstawowego twierdzenia analizy (analizy twierdzenie podstawowe), można wygodnie i zwięźle opisać jako przypadki szczególne twierdzenia Stokesa.
i związane z nim grupy kohomologii de Rhama odgrywają ważną rolę w geometrii różniczkowej i topologii algebraicznej; dzięki wprowadzeniu języka f.r. różne wzory całkowe analizy wektorowej, będące uogólnieniami podstawowego twierdzenia analizy (analizy twierdzenie podstawowe), można wygodnie i zwięźle opisać jako przypadki szczególne twierdzenia Stokesa.
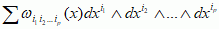 , gdzie sumowanie rozciąga się na wszystkie układy indeksów 1≤ i1 < i2 < ... < ip ≤ n; zbiór wszystkich f.r. stopnia p na rozmaitości M oznacza się symbolem Ωp(M); tzw. kompleks de Rhama
, gdzie sumowanie rozciąga się na wszystkie układy indeksów 1≤ i1 < i2 < ... < ip ≤ n; zbiór wszystkich f.r. stopnia p na rozmaitości M oznacza się symbolem Ωp(M); tzw. kompleks de Rhama 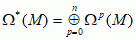 i związane z nim grupy kohomologii de Rhama odgrywają ważną rolę w geometrii różniczkowej i topologii algebraicznej; dzięki wprowadzeniu języka f.r. różne wzory całkowe analizy wektorowej, będące uogólnieniami podstawowego twierdzenia analizy (analizy twierdzenie podstawowe), można wygodnie i zwięźle opisać jako przypadki szczególne twierdzenia Stokesa.
i związane z nim grupy kohomologii de Rhama odgrywają ważną rolę w geometrii różniczkowej i topologii algebraicznej; dzięki wprowadzeniu języka f.r. różne wzory całkowe analizy wektorowej, będące uogólnieniami podstawowego twierdzenia analizy (analizy twierdzenie podstawowe), można wygodnie i zwięźle opisać jako przypadki szczególne twierdzenia Stokesa. 

