Stokesa twierdzenie
Encyklopedia PWN
; twierdzenie wiążące całkę krzywoliniową po zorientowanej krzywej zamkniętej K z całką po zorientowanej powierzchni D ograniczonej krzywą K: jeśli funkcje P, Q, R mają ciągłe pochodne cząstkowe, a orientacje K i D są zgodne, to
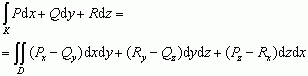 lub (w formie wektorowej)
lub (w formie wektorowej)
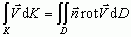 , gdzie
, gdzie 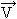 = [P, Q, R],
= [P, Q, R], 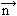 — pole wersorów normalnych, dK — element krzywej, dD — element powierzchni.
— pole wersorów normalnych, dK — element krzywej, dD — element powierzchni.
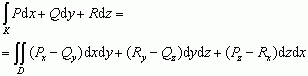 lub (w formie wektorowej)
lub (w formie wektorowej) 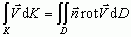 , gdzie
, gdzie 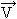 = [P, Q, R],
= [P, Q, R], 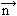 — pole wersorów normalnych, dK — element krzywej, dD — element powierzchni.
— pole wersorów normalnych, dK — element krzywej, dD — element powierzchni.

