forma
mat. wielomian jednorodny wielu zmiennych, czyli wyrażenie postaci [łac.],
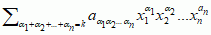 , gdzie
, gdzie 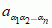 — dowolne liczby (współczynniki f.), α1, α2, ... , αn — nieujemne liczby całkowite, k — stopień f., a sumowanie przebiega wszystkie różne układy liczb α1, α2, ... , αn, dla których α1 + α2 + ... + αn = k;
— dowolne liczby (współczynniki f.), α1, α2, ... , αn — nieujemne liczby całkowite, k — stopień f., a sumowanie przebiega wszystkie różne układy liczb α1, α2, ... , αn, dla których α1 + α2 + ... + αn = k;

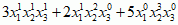 jest trójkową formą sześcienną — są 3 zmienne x1, x2, x3 i stopień k = 3 (x0 = 1). Formą
jest trójkową formą sześcienną — są 3 zmienne x1, x2, x3 i stopień k = 3 (x0 = 1). Formą 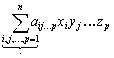 ,
, 
