wektorowy rachunek
Encyklopedia PWN
Rachunek wektorowy dzieli się na algebrę wektorową oraz analizę wektorową. Zbiór wektorów (np. trójwymiarowych, tzn. o trzech składowych) stanowi przestrzeń wektorową (liniową), co oznacza, że wektory można dodawać oraz mnożyć przez liczby, otrzymując w rezultacie tych działań nowe wektory, przy czym spełnione muszą być wszystkie aksjomaty liniowej przestrzeni; wektory  i
i  dodaje się tworząc tzw. wypadkową
dodaje się tworząc tzw. wypadkową  +
+  ; różnicę wektorów
; różnicę wektorów  i
i  otrzymuje się łącząc końce wektorów
otrzymuje się łącząc końce wektorów  i
i  i stawiając „strzałkę” zwrotu przy odjemnej; działania te pozwalają wprowadzić pojęcie kombinacji liniowej wektorów
i stawiając „strzałkę” zwrotu przy odjemnej; działania te pozwalają wprowadzić pojęcie kombinacji liniowej wektorów  ,
,  ,
, 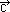 , tzn. wyrażenia postaci λ
, tzn. wyrażenia postaci λ + µ
+ µ + ν
+ ν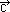 (λ, µ, ν — liczby); wektory
(λ, µ, ν — liczby); wektory  ,
,  ,
, 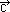 nazywają się liniowo niezależne, jeżeli z warunku λ
nazywają się liniowo niezależne, jeżeli z warunku λ + µ
+ µ + ν
+ ν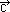 = 0 wynika, że λ = µ = ν = 0; natomiast jeżeli istnieją takie 3 liczby λ, µ, ν (nie wszystkie jednocześnie równe zeru), że λ
= 0 wynika, że λ = µ = ν = 0; natomiast jeżeli istnieją takie 3 liczby λ, µ, ν (nie wszystkie jednocześnie równe zeru), że λ + µ
+ µ + ν
+ ν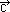 = 0, to wektory
= 0, to wektory  ,
,  ,
, 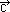 nazywają się liniowo zależne i wtedy każdy z nich można wyrazić jako pewną kombinację liniową pozostałych, co geometrycznie oznacza, że wektory te są równoległe do jednej płaszczyzny; 3 wektory
nazywają się liniowo zależne i wtedy każdy z nich można wyrazić jako pewną kombinację liniową pozostałych, co geometrycznie oznacza, że wektory te są równoległe do jednej płaszczyzny; 3 wektory 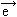 1,
1, 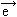 2,
2, 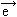 3 liniowo niezależne i o wspólnym początku tworzą tzw. bazę trójwymiarową przestrzeni wektorowej, co oznacza, że każdy wektor
3 liniowo niezależne i o wspólnym początku tworzą tzw. bazę trójwymiarową przestrzeni wektorowej, co oznacza, że każdy wektor 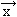 tej przestrzeni da się zapisać jako kombinacja liniowa wektorów bazy:
tej przestrzeni da się zapisać jako kombinacja liniowa wektorów bazy: 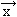 = x1
= x1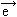 1 + x2
1 + x2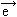 2 + x3
2 + x3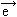 3, gdzie liczby x1, x2, x3 nazywają się współrzędnymi (składowymi) wektora
3, gdzie liczby x1, x2, x3 nazywają się współrzędnymi (składowymi) wektora 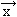 ; wszystkie operacje na wektorach można również zdefiniować za pomocą współrzędnych, np. iloczyn skalarny wektorów
; wszystkie operacje na wektorach można również zdefiniować za pomocą współrzędnych, np. iloczyn skalarny wektorów  (ax, ay, az) i
(ax, ay, az) i  (bx, by, bz) w bazie prostokątnej:
(bx, by, bz) w bazie prostokątnej: 
 = axbx + ayby + azbz lub kąt φ między wektorami:
= axbx + ayby + azbz lub kąt φ między wektorami:
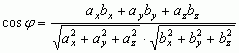 .
.
 i
i  dodaje się tworząc tzw. wypadkową
dodaje się tworząc tzw. wypadkową  +
+  ; różnicę wektorów
; różnicę wektorów  i
i  otrzymuje się łącząc końce wektorów
otrzymuje się łącząc końce wektorów  i
i  i stawiając „strzałkę” zwrotu przy odjemnej; działania te pozwalają wprowadzić pojęcie kombinacji liniowej wektorów
i stawiając „strzałkę” zwrotu przy odjemnej; działania te pozwalają wprowadzić pojęcie kombinacji liniowej wektorów  ,
,  ,
, 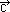 , tzn. wyrażenia postaci λ
, tzn. wyrażenia postaci λ + µ
+ µ + ν
+ ν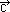 (λ, µ, ν — liczby); wektory
(λ, µ, ν — liczby); wektory  ,
,  ,
, 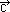 nazywają się liniowo niezależne, jeżeli z warunku λ
nazywają się liniowo niezależne, jeżeli z warunku λ + µ
+ µ + ν
+ ν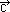 = 0 wynika, że λ = µ = ν = 0; natomiast jeżeli istnieją takie 3 liczby λ, µ, ν (nie wszystkie jednocześnie równe zeru), że λ
= 0 wynika, że λ = µ = ν = 0; natomiast jeżeli istnieją takie 3 liczby λ, µ, ν (nie wszystkie jednocześnie równe zeru), że λ + µ
+ µ + ν
+ ν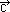 = 0, to wektory
= 0, to wektory  ,
,  ,
, 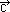 nazywają się liniowo zależne i wtedy każdy z nich można wyrazić jako pewną kombinację liniową pozostałych, co geometrycznie oznacza, że wektory te są równoległe do jednej płaszczyzny; 3 wektory
nazywają się liniowo zależne i wtedy każdy z nich można wyrazić jako pewną kombinację liniową pozostałych, co geometrycznie oznacza, że wektory te są równoległe do jednej płaszczyzny; 3 wektory 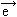 1,
1, 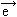 2,
2, 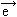 3 liniowo niezależne i o wspólnym początku tworzą tzw. bazę trójwymiarową przestrzeni wektorowej, co oznacza, że każdy wektor
3 liniowo niezależne i o wspólnym początku tworzą tzw. bazę trójwymiarową przestrzeni wektorowej, co oznacza, że każdy wektor 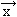 tej przestrzeni da się zapisać jako kombinacja liniowa wektorów bazy:
tej przestrzeni da się zapisać jako kombinacja liniowa wektorów bazy: 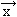 = x1
= x1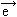 1 + x2
1 + x2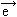 2 + x3
2 + x3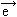 3, gdzie liczby x1, x2, x3 nazywają się współrzędnymi (składowymi) wektora
3, gdzie liczby x1, x2, x3 nazywają się współrzędnymi (składowymi) wektora 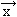 ; wszystkie operacje na wektorach można również zdefiniować za pomocą współrzędnych, np. iloczyn skalarny wektorów
; wszystkie operacje na wektorach można również zdefiniować za pomocą współrzędnych, np. iloczyn skalarny wektorów  (ax, ay, az) i
(ax, ay, az) i  (bx, by, bz) w bazie prostokątnej:
(bx, by, bz) w bazie prostokątnej: 
 = axbx + ayby + azbz lub kąt φ między wektorami:
= axbx + ayby + azbz lub kąt φ między wektorami: 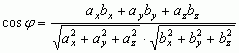 .
. W analizie wektorowej rozpatruje się pola skalarne i pola wektorowe oraz rozmaite operacje różniczkowe określone dla tych pól, jak również operacje całkowe; do najważniejszych operacji różniczkowych w rachunku wektorowym należą: gradient, dywergencja, rotacja; operacje te z jednych pól pozwalają, przez różniczkowanie, otrzymywać nowe pola, np. z pola skalarnego f(P) można otrzymać pole wektorowe grad f(P), a z pola wektorowego  (P) — pole skalarne div
(P) — pole skalarne div  (P); do najważniejszych operacji całkowych należą: całka ciśn. skalara f na powierzchnię S, czyli całka
(P); do najważniejszych operacji całkowych należą: całka ciśn. skalara f na powierzchnię S, czyli całka 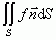 (
(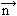 — wektor zewn. normalny do powierzchni S), krążenie pola wektorowego
— wektor zewn. normalny do powierzchni S), krążenie pola wektorowego  (P) wzdłuż zamkniętego konturu L, czyli całka
(P) wzdłuż zamkniętego konturu L, czyli całka 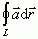 (
(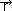 — wektor wodzący konturu L), strumień pola wektorowego
— wektor wodzący konturu L), strumień pola wektorowego  (P) przez powierzchnię S, czyli całka
(P) przez powierzchnię S, czyli całka 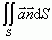 .
.
 (P) — pole skalarne div
(P) — pole skalarne div  (P); do najważniejszych operacji całkowych należą: całka ciśn. skalara f na powierzchnię S, czyli całka
(P); do najważniejszych operacji całkowych należą: całka ciśn. skalara f na powierzchnię S, czyli całka 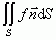 (
(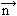 — wektor zewn. normalny do powierzchni S), krążenie pola wektorowego
— wektor zewn. normalny do powierzchni S), krążenie pola wektorowego  (P) wzdłuż zamkniętego konturu L, czyli całka
(P) wzdłuż zamkniętego konturu L, czyli całka 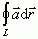 (
(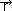 — wektor wodzący konturu L), strumień pola wektorowego
— wektor wodzący konturu L), strumień pola wektorowego  (P) przez powierzchnię S, czyli całka
(P) przez powierzchnię S, czyli całka 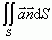 .
. Wyszczególnione operacje różniczkowe i całkowe występują w ważnych twierdzeniach rachunku wektorowego, mianowicie w twierdzeniu Greena i we wzorach Gaussa–Ostrogradskiego i Stokesa, które odgrywają podstawową rolę w zastosowaniach fiz. i technicznych. Rachunek wektorowy ukształtował się w samodzielną dyscyplinę w poł. XIX w. dzięki pracom: H.G. Grassmanna, W.R. Hamiltona, J. Maxwella i J.W. Gibbsa.


