iloczyn mieszany wektorów,
mat. pojęcie z zakresu rachunku wektorowego (w przestrzeni euklidesowej): i.m.w.  ,
,  ,
, 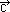 o wspólnym początku jest iloczyn skalarny (
o wspólnym początku jest iloczyn skalarny ( ×
×  ) ·
) · 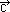 , gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);
, gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);

 , gdzie ai, bi, ci (i = 1, 2, 3) są współrz. (składowymi) danych wektorów; zachodzą zależności: (
, gdzie ai, bi, ci (i = 1, 2, 3) są współrz. (składowymi) danych wektorów; zachodzą zależności: (
