mieszane
Encyklopedia PWN
mat. własność niektórych układów dynamicznych (X, T) odpowiadająca równomiernemu rozprowadzaniu (wymieszaniu) zawartości każdego typowego podzbioru przestrzeni X w całej objętości tej przestrzeni przy wielokrotnym powtarzaniu przekształcenia T. Terminem „mieszanie” nazywa się także sam układ dynamiczny mający własność m. lub działające w nim przekształcenie T. M. jest własnością silniejszą od ergodyczności, która wyraża jedynie nieistnienie istotnie mniejszego podukładu zawartego w (X, T). Intuicyjnemu pojmowaniu równomiernego rozprowadzania odpowiada następująca mat. definicja: jeśli T: X → X jest mierzalnym przekształceniem przestrzeni X w siebie, zachowującym miarę probabilistyczną P (tzn. P(T–1(A)) = P(A) dla każdego mierzalnego podzbioru A zawartego w X), to układ (X, T) ma własność m., gdy dla wszystkich mierzalnych podzbiorów A, B (tj. tych, których prawdopodobieństwa da się określić) zachodzi równość 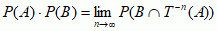 .
.
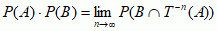 .
.
wprawianie w ruch danego ośrodka w celu uzyskania emulsji, zawiesiny ciał stałych lub przyspieszenia niektórych procesów (np. ekstrakcji, absorpcji, wymiany ciepła, rozpuszczania);
ekon. jeden z głównych typów gospodarek, wyróżniony ze względu na rodzaj regulacji procesów gospodarczych.
mat. pojęcie z zakresu rachunku wektorowego (w przestrzeni euklidesowej): i.m.w.  ,
,  ,
, 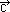 o wspólnym początku jest iloczyn skalarny (
o wspólnym początku jest iloczyn skalarny ( ×
×  ) ·
) · 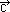 , gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);
, gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);
 ,
,  ,
, 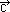 o wspólnym początku jest iloczyn skalarny (
o wspólnym początku jest iloczyn skalarny ( ×
×  ) ·
) · 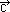 , gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);
, gdzie znak × oznacza mnożenie wektorowe (iloczyn wektorowy), a znak · oznacza mnożenie skalarne (iloczyn skalarny);
powstawanie wrażeń barwnych przez składanie (mieszanie) barw prostych w oku;
rodzaj → gazu generatorowego.


