informacji teoria

informacji teoria,

teoria przekazywania wiadomości ze źródła wiadomości do obiektu ich przeznaczenia — odbiorcy (ujścia);

w szerszym znaczeniu także nauka zajmująca się wszechstronną analizą procesów przekazywania informacji za pomocą systemów znakowych w społeczeństwie oraz w zbiorowościach biologicznych. Wiadomość może być przesyłana w przestrzeni od nadawcy do odbiorcy, a także podlegać rejestracji (zapamiętywaniu). Rozróżnia się źródła: ciągłe — podające dowolne wiadomości z ciągłego ich zbioru (np. wskazania termometru rtęciowego), oraz ziarniste (dyskretne) — podające jedną spośród skończonej liczby wiadomości (np. źródło podające litery); do tych ostatnich należą źródła binarne — podające jedną z 2 możliwych wiadomości (np. element log. o 2 wyróżnionych stanach: „tak” i „nie”). Ponieważ wiadomość przed wyemitowaniem jej przez źródło nie jest znana odbiorcy, traktuje się ją jako wielkość losową. Miarą niewiedzy o tym, jaką konkretną wiadomość wyemituje źródło ziarniste (tj. miarą ilości informacji zawartej w poszczególnych możliwych wiadomościach emitowanych przez to źródło) jest wielkość, zw. 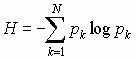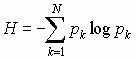entropią źródła, równa wartości średniej ilości informacji przypadającej na pojedynczą wiadomość: , gdzie N jest liczbą możliwych wiadomości, p_k — prawdopodobieństwem emisji k-tej wiadomości. Im większa jest niewiedza o tym, jaką wiadomość wyemituje źródło, tym więcej informacji uzyska się, otrzymując ze źródła konkretną wiadomość. Ilość informacji zawarta w k-tej wiadomości jest równa I_k = – log_a p_k. Jeśli prawdopodobieństwo emisji poszczególnych wiadomości jest jednakowe p₁ = ... = p_k = p, to ilość informacji zawartej w każdej z nich I= log_a 1/p = log_a N i osiąga maks. wartość. Jednostką ilości informacji (log_a 1/p = 1) wg normy ISO jest szanon, Sh (we wzorze występuje logarytm przy podstawie a = 2); stosuje się też: hartlej (logarytm przy podstawie 10), naturalną jednostkę, dawniej zw. nitem (logarytm przy podstawie e), przy czym 1 Sh= 0,301 hartleja = 0,693 naturalnej jednostki; np., jeśli źródło binarne może emitować tylko 1 wiadomość z prawdopodobieństwem 1, to wiadomość ta zawiera 0 Sh informacji (log₂ 1 = 0), jeśli może emitować 2 wiadomości z jednakowymi prawdopodobieństwami, to każda wiadomość zawiera 1 Sh (log₂ 2 = 1) itd. Dla samej techniki przekazywania wiadomości nieistotny jest ich semantyczny aspekt (sens, znaczenie, prawdziwość) oraz cel przekazywania, natomiast ma znaczenie rodzaj elementów informacyjnych i statyst. rozkład ich emisji oraz wierność, szybkość i ekonomiczność przekazu.

Zwykle w celu przekazania wiadomości przyporządkowuje się jej (w nadajniku) pewien nośnik zw. sygnałem nadawanym, np. wiadomościom-słowom przyporządkowuje się dźwięki mowy, drukowane wyrazy lub modulowane sygnały radiowe (sygnał); w technice największą rolę odgrywają sygnały elektr., które są poddawane modulacji lub kodowaniu. Nadawane sygnały docierają do odbiornika za pośrednictwem zespołu środków zw. kanałem komunikacyjnym, ulegając przy tym zniekształceniom (tłumienie, zakłócenia). Zadaniem odbiornika jest możliwie wierne odtworzenie nadanej wiadomości i przekazanie jej odbiorcy. W przypadku sygnałów cyfrowych proces przesyłania wiadomości charakteryzuje wielkość zw. przepływnością (szybkością) bitową, określona liczbą elementów sygnału (np. 0 i 1) przesyłanych kanałem telekomunik. w ciągu 1 s (wyrażana w bit/s).

Odtwarzanie nadanej wiadomości odbywa się w 2 etapach; pierwszy polega na odtworzeniu sygnału nadanego na podstawie sygnału odebranego, drugi — na wskazaniu wiadomości na podstawie sygnału odtworzonego. Dopasowanie sygnału odebranego do nadanego w warunkach występowania nieznanych (przypadkowych) zniekształceń nadanego sygnału w kanale komunik. jest problemem wyboru (decyzyjnym); kryterium jakości odbioru jest powiązane z kryterium podejmowania pojedynczej decyzji (decyzji teoria, gier teoria). Takie powiązanie pozwala na ustalenie kryterium jakości reguły odbioru (sposobu odtwarzania).

Współczesna t.i. obejmuje: teorię modeli matematycznych źródeł informacji i źródeł zakłóceń, teorię zajmującą się miarą ilości przekazywanej informacji oraz właściwościami transmisyjnymi kanału komunik., teorię kodowania i statyst. teorię detekcji (odtwarzania sygnału). Ważnym działem t.i. jest teoria obróbki danych, zajmująca się wstępnym przekształcaniem postaci wiadomości w postać dogodną do dalszych przekształceń. T.i. znajduje zastosowanie w telekomunikacji i w teoret. badaniach w wielu dziedzinach, zwłaszcza w lingwistyce, ekonomii i biologii.

Podstawy ogólne t.i. opracował 1928 R.W.L. Hartley, a rozwinął je 1944 C.E. Shannon; znaczny wkład w rozwój t.i. wniosły prace: N. Wienera (ok. 1940), A. Kołmogorowa (1941), A. Chinczina, W. Kotielnikowa (1933, 1947), D. Middletona (1954, 1960), w Polsce — J. Seidlera.

Bibliografia

J. Seidler Statystyczna teoria odbioru sygnałów, Warszawa 1963;

tegoż Systemy przesyłania informacji cyfrowych, Warszawa 1972;

K. Szaniawski Filozofia i nauka. Zarys encyklopedyczny, Wrocław 1987;

B.O. Küpers Geneza informacji biologicznej, Warszawa 1991.

C.E. Shannon, W. Weaver The Mathematical Theory of Communication, Urbana 1949.