średnia,
mat. liczba charakteryzująca w pewien określony sposób n liczb: a1, a2, ... , an, zawarta między najmniejszą i największą z tych liczb;
średnia
Encyklopedia PWN
do najczęściej stosowanych ś. należą: 1) ś. potęgowa (rzędu k) liczb dodatnich — liczba 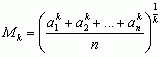 , gdzie k ≠ 0; liczbę
, gdzie k ≠ 0; liczbę 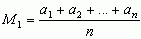 nazywa się ś. arytmetyczną, liczbę
nazywa się ś. arytmetyczną, liczbę 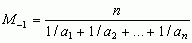 ś. harmoniczną, liczbę
ś. harmoniczną, liczbę 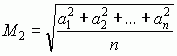 — ś. kwadratową, liczbę
— ś. kwadratową, liczbę 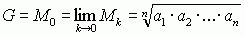 — ś. geometryczną (lub proporcjonalną); istnieją granice:
— ś. geometryczną (lub proporcjonalną); istnieją granice: 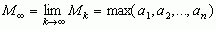 oraz
oraz 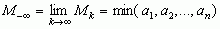 (max i min oznaczają odpowiednio największą i najmniejszą z liczb a1, a2, ... , an); dla k < p zachodzi relacja Mk ≤ Mp (Mk = Mp, gdy a1 = a2 = ... = an); zachodzą nierówności: min(a1, a2, ... , an) ≤ M–1 ≤ G ≤ M1 ≤ M2 ≤ max(a1, a2, ... , an); 2) ś. arytmetyczno-geometryczna liczb dodatnich — wspólna granica ciągów liczbowych {xn} i {yn}, gdzie
(max i min oznaczają odpowiednio największą i najmniejszą z liczb a1, a2, ... , an); dla k < p zachodzi relacja Mk ≤ Mp (Mk = Mp, gdy a1 = a2 = ... = an); zachodzą nierówności: min(a1, a2, ... , an) ≤ M–1 ≤ G ≤ M1 ≤ M2 ≤ max(a1, a2, ... , an); 2) ś. arytmetyczno-geometryczna liczb dodatnich — wspólna granica ciągów liczbowych {xn} i {yn}, gdzie 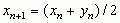 oraz
oraz 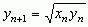 (n = 1, 2, ...); 3) ś. ważona (z wagami, tj. przyjętymi dodatnimi parametrami p1, p2, ... , pn) — liczba
(n = 1, 2, ...); 3) ś. ważona (z wagami, tj. przyjętymi dodatnimi parametrami p1, p2, ... , pn) — liczba 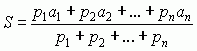 ; 4) ś. logarytmiczna między 2 wartościami x1 i x2 — liczba
; 4) ś. logarytmiczna między 2 wartościami x1 i x2 — liczba 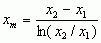 .
.
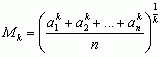 , gdzie k ≠ 0; liczbę
, gdzie k ≠ 0; liczbę 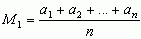 nazywa się ś. arytmetyczną, liczbę
nazywa się ś. arytmetyczną, liczbę 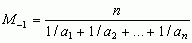 ś. harmoniczną, liczbę
ś. harmoniczną, liczbę 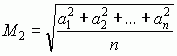 — ś. kwadratową, liczbę
— ś. kwadratową, liczbę 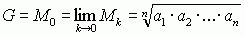 — ś. geometryczną (lub proporcjonalną); istnieją granice:
— ś. geometryczną (lub proporcjonalną); istnieją granice: 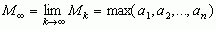 oraz
oraz 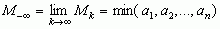 (max i min oznaczają odpowiednio największą i najmniejszą z liczb a1, a2, ... , an); dla k < p zachodzi relacja Mk ≤ Mp (Mk = Mp, gdy a1 = a2 = ... = an); zachodzą nierówności: min(a1, a2, ... , an) ≤ M–1 ≤ G ≤ M1 ≤ M2 ≤ max(a1, a2, ... , an); 2) ś. arytmetyczno-geometryczna liczb dodatnich — wspólna granica ciągów liczbowych {xn} i {yn}, gdzie
(max i min oznaczają odpowiednio największą i najmniejszą z liczb a1, a2, ... , an); dla k < p zachodzi relacja Mk ≤ Mp (Mk = Mp, gdy a1 = a2 = ... = an); zachodzą nierówności: min(a1, a2, ... , an) ≤ M–1 ≤ G ≤ M1 ≤ M2 ≤ max(a1, a2, ... , an); 2) ś. arytmetyczno-geometryczna liczb dodatnich — wspólna granica ciągów liczbowych {xn} i {yn}, gdzie 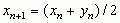 oraz
oraz 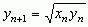 (n = 1, 2, ...); 3) ś. ważona (z wagami, tj. przyjętymi dodatnimi parametrami p1, p2, ... , pn) — liczba
(n = 1, 2, ...); 3) ś. ważona (z wagami, tj. przyjętymi dodatnimi parametrami p1, p2, ... , pn) — liczba 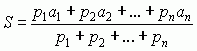 ; 4) ś. logarytmiczna między 2 wartościami x1 i x2 — liczba
; 4) ś. logarytmiczna między 2 wartościami x1 i x2 — liczba 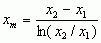 .
. Średnie (również innych rodzajów) wykorzystuje się w rachunku prawdopodobieństwa i statystyce (m.in. wartość oczekiwana, odchylenie standardowe, mediana) oraz w dyscyplinach doświadczalnych i technicznych.


