drgania sieci krystalicznej,
drgania (o małej amplitudzie) atomów tworzących sieć krystaliczną wokół ich położeń równowagi.
drgania sieci krystalicznej
Encyklopedia PWN
Zbiór wszystkich częst. tych drgań tworzy tzw. widmo drgań normalnych sieci. Częstości drgań normalnych zawierają się w ograniczonym przedziale wartości między zerem i pewną maks. częst. ωm, zależną od mas atomów tworzących kryształ i od sił ich wzajemnego oddziaływania. Liczba niezależnych drgań normalnych jest równa liczbie współrzędnych atomów, tj. 3Nr dla kryształu zawierającego N komórek elementarnych i r atomów w każdej komórce. W ogólnym przypadku stan drgań kryształu jest opisany superpozycją drgań normalnych. Pojedyncze drganie normalne można przedstawić jako falę płaską scharakteryzowaną wektorem falowym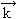 
, częst. ω(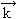, s) i wektorem polaryzacji 
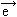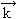j(, s). Wektor falowy o wartości k = 2π/λ (λ — długość fali) określa kierunek rozchodzenia się fali, wektor polaryzacji — kierunek drgań poszczególnych atomów w komórce elementarnej (numerowany wskaźnikiem j = 1, 2, ... , r). Każdemu wektorowi falowemu odpowiada kilka drgań normalnych o różnych częst. (numerowane wskaźnikiem s = 1, 2, ... , 3r). Wykresy zależności częst. ω od wektora 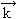dla wybranego kierunku rozchodzenia się fali noszą nazwę krzywych dyspersji i składają się z 3r linii zw. gałęziami (rys.). Trzem spośród nich (dla małych wartości k, tj. dla długości fal dużych w porównaniu z odległością między atomami) odpowiada zależność, zw. liniowym prawem dyspersji: ω(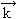, s) = vsk (tj. ω(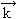, s) = 0 dla k = 0; vs — stały współczynnik). Krzywe te noszą nazwę gałęzi akustycznych i odpowiadają drganiom komórki elementarnej jako całości. W przypadku pozostałych 3(r–1) krzywych dyspersji ω(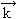, s) ≠ 0 dla k = 0, przy czym drgania atomów zachodzą w taki sposób, że środek masy każdej komórki elementarnej pozostaje w spoczynku. Jeżeli w komórce elementarnej znajdują się jony przeciwnego znaku, to tego rodzaju ruch można wywołać np. falą elektromagnetyczną o częst. zwykle z zakresu podczerwieni; dlatego też gałęzie te są nazywane gałęziami optycznymi. Drganiami akustycznymi są np. drgania cieplne w niskich temperaturach, fale dźwiękowe; odznaczają się one małą częst. (od 0 do ok. 1012 Hz). Natomiast drgania opt., związane ze zjawiskami elektromagnetycznymi, odznaczają się stosunkowo dużą częst. (rzędu 1013 Hz).
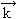, częst. ω(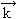, s) i wektorem polaryzacji 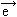j(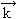, s). Wektor falowy o wartości k = 2π/λ (λ — długość fali) określa kierunek rozchodzenia się fali, wektor polaryzacji — kierunek drgań poszczególnych atomów w komórce elementarnej (numerowany wskaźnikiem j = 1, 2, ... , r). Każdemu wektorowi falowemu odpowiada kilka drgań normalnych o różnych częst. (numerowane wskaźnikiem s = 1, 2, ... , 3r). Wykresy zależności częst. ω od wektora 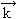dla wybranego kierunku rozchodzenia się fali noszą nazwę krzywych dyspersji i składają się z 3r linii zw. gałęziami (rys.). Trzem spośród nich (dla małych wartości k, tj. dla długości fal dużych w porównaniu z odległością między atomami) odpowiada zależność, zw. liniowym prawem dyspersji: ω(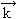, s) = vsk (tj. ω(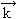, s) = 0 dla k = 0; vs — stały współczynnik). Krzywe te noszą nazwę gałęzi akustycznych i odpowiadają drganiom komórki elementarnej jako całości. W przypadku pozostałych 3(r–1) krzywych dyspersji ω(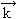, s) ≠ 0 dla k = 0, przy czym drgania atomów zachodzą w taki sposób, że środek masy każdej komórki elementarnej pozostaje w spoczynku. Jeżeli w komórce elementarnej znajdują się jony przeciwnego znaku, to tego rodzaju ruch można wywołać np. falą elektromagnetyczną o częst. zwykle z zakresu podczerwieni; dlatego też gałęzie te są nazywane gałęziami optycznymi. Drganiami akustycznymi są np. drgania cieplne w niskich temperaturach, fale dźwiękowe; odznaczają się one małą częst. (od 0 do ok. 1012 Hz). Natomiast drgania opt., związane ze zjawiskami elektromagnetycznymi, odznaczają się stosunkowo dużą częst. (rzędu 1013 Hz). Opis ten odnosi się do idealnych kryształów. Obecność defektów w rzeczywistym krysztale powoduje istotne zmiany w obrazie drgań. Na przykład widmo częst. drgań kryształu domieszkowanego atomami lżejszymi niż atomy sieci składa się z pasma oraz z pojedynczej linii leżącej powyżej wierzchołka pasma, odpowiadającej tzw. drganiu lokalnemu o amplitudzie malejącej wykładniczo ze wzrostem odległości od atomu domieszki. W przypadku domieszkowania atomami cięższymi od atomów sieci może wystąpić tzw. drganie rezonansowe, czyli rezonansowy wzrost amplitudy drgań o określonej częst., znajdującej się wewnątrz pasma.
Podany model d.s.k. całkowicie opiera się na prawach mechaniki klas., nie tłumaczy jednak pewnych właściwości ciał stałych i zachodzących w nich procesów, które można wyjaśnić jedynie za pomocą opisu kwantowego. Kwant energii d.s.k. jest nazywany fononem (przez analogię z fotonem, czyli kwantem pola elektromagnetycznego). Pojedynczy fonon jest odpowiednikiem klas. drgania normalnego, jest więc określony wektorem falowym, częst. drgania normalnego oraz wektorem polaryzacji. W oddziaływaniach z elektronami, neutronami, fotonami czy oddziaływaniach fonon–fonon zachowuje się on jak kwazicząstka o energii ℏω(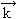, s) i kwazipędzie ℏ 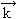(ℏ = h/2π, gdzie h — stała Plancka). Opis d.s.k. za pomocą fononów pozwala na wyjaśnienie właściwości cieplnych ciał stałych w niskich temperaturach (Debye’a model), a także wielu zagadnień dotyczących wzajemnego oddziaływania różnych cząstek z drganiami atomów w krysztale, np. rozpraszania elektronów na d.s.k. w metalach i półprzewodnikach, rozpraszania neutronów i promieni rentgenowskich, zjawiska absorpcji w podczerwieni. Dzięki uwzględnieniu oddziaływania elektronów z fononami zostało wyjaśnione zjawisko nadprzewodnictwa niskotemperaturowego.
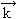, s) i kwazipędzie ℏ 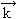(ℏ = h/2π, gdzie h — stała Plancka). Opis d.s.k. za pomocą fononów pozwala na wyjaśnienie właściwości cieplnych ciał stałych w niskich temperaturach (Debye’a model), a także wielu zagadnień dotyczących wzajemnego oddziaływania różnych cząstek z drganiami atomów w krysztale, np. rozpraszania elektronów na d.s.k. w metalach i półprzewodnikach, rozpraszania neutronów i promieni rentgenowskich, zjawiska absorpcji w podczerwieni. Dzięki uwzględnieniu oddziaływania elektronów z fononami zostało wyjaśnione zjawisko nadprzewodnictwa niskotemperaturowego. Bezpośrednie obliczenie częst. drgań normalnych dla konkretnych substancji krystalicznych stanowi skomplikowany problem fizyki teoretycznej. Doświadczalne metody wyznaczania widma częst. opierają się na badaniu rozpraszania powolnych neutronów, absorpcji promieniowania podczerwonego, rozpraszania ramanowskiego i in. zjawisk.
Eugenia Kaczmarek-Morawiec
