Maxwella równania,
podstawowe równania elektrodynamiki klas. określające związek między wielkościami charakteryzującymi pole elektromagnetyczne w dowolnym ośrodku (w tym w próżni) a jego źródłami, czyli ładunkami i prądami elektrycznymi.
- krążenie
- szczególna teoria względności
- elektrodynamika
- elektrodynamika kwantowa
- elektrostatyka
- fale
- fale elektromagnetyczne
- falowód
- fizyki prawa
- klasyczna teoria pola
- kwantowa teoria pola
- Maxwell James (Clerk)
- optyka
- optyka elektronowa
- optyka falowa
- optyka nieliniowa
- pole elektromagnetyczne
- potencjały pola elektromagnetycznego
- prąd przesunięcia
- rotacja
- superpozycji zasada
- względności teoria
- magnetyzm
- pole fizyczne
- pole elektryczne
- pole magnetyczne
- Ampère’a prawo

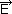 = – ∂
= – ∂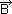 /∂t (prawo indukcji elektromagnetycznej Faradaya),
/∂t (prawo indukcji elektromagnetycznej Faradaya), 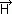 =
= 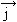 + (∂
+ (∂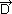 /∂t) (prawo Ampére’a uzupełnione przez J. Maxwella),
/∂t) (prawo Ampére’a uzupełnione przez J. Maxwella), 
