kinetyczna teoria gazów,
teoria zajmująca się opisem, na gruncie teorii klas., rozróżnialnych cząsteczek rozrzedzonego gazu;
kinetyczna teoria gazów
Encyklopedia PWN
w k.t.g. zakłada się, że: średnia odległość między cząsteczkami jest znacznie większa niż efektywny zasięg potencjałów oddziaływań, cząsteczki oddziałują ze sobą wskutek zderzeń (opisywanych przez różniczkowy przekrój czynny), ścianki naczynia, które gaz wypełnia odbijają cząsteczki sprężyście. Stany poszczególnych cząsteczek traktuje się jako statystycznie niezależne (postulat chaosu molekularnego), a gaz opisuje jedną funkcją rozkładu f(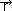 ,
, 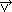 , t), gdzie f(
, t), gdzie f(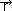 ,
, 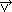 , t)d3rd3v jest liczbą cząsteczek, które w chwili t znajdują się w małym elemencie objętości przestrzeni fazowej d3rd3v wokół punktu (
, t)d3rd3v jest liczbą cząsteczek, które w chwili t znajdują się w małym elemencie objętości przestrzeni fazowej d3rd3v wokół punktu (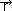 ,
, 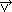 ). Czasową ewolucję funkcji rozkładu opisuje kinetyczne równanie Boltzmanna. Dla gazu w stanie równowagi termodynamicznej f przyjmuje postać rozkładu Maxwella. Znajomość f pozwala obliczać wszystkie wielkości termodynamiczne, np.: średni kwadrat prędkości cząsteczek <
). Czasową ewolucję funkcji rozkładu opisuje kinetyczne równanie Boltzmanna. Dla gazu w stanie równowagi termodynamicznej f przyjmuje postać rozkładu Maxwella. Znajomość f pozwala obliczać wszystkie wielkości termodynamiczne, np.: średni kwadrat prędkości cząsteczek <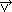 2> = 3kBT/m (kB — stała Boltzmanna, m — masa cząsteczki gazu, T — temperatura), która jest miarą temperatury; na każdy stopień swobody (stopnie swobody) jednej cząsteczki przypada średnio energia kBT/2 (ekwipartycji energii zasada). Gdy gaz nie jest w równowadze (postać f różni się od postaci rozkładu Maxwella) — na ogół temperatura, gęstość i średnia prędkość cząsteczek nie są stałe w całej objętości jaką zajmuje gaz. Gaz dąży do osiągnięcia równowagi przez wyrównanie wartości tych parametrów; zachodzi to za pośrednictwem lokalnych przekazów energii, masy i pędu (transport). Mechanizmem prowadzącym do takich przekazów w rozrzedzonym gazie są zderzenia binarne cząsteczek. Średnia droga pojedynczej cząsteczki między dwoma kolejnymi zderzeniami nosi nazwę drogi swobodnej. Dla gazu nierównowagowego znajdującego się blisko stanu równowagi przyjmuje się, że w zerowym przybliżeniu rozkład Maxwella jest spełniony lokalnie, tzn. układ jest scharakteryzowany przez lokalną temperaturę (zależną od położenia cząsteczek i czasu). Pozwala to na wyprowadzenie równań hydrodynamiki dla przepływu gazu bez uwzględnienia lepkości. W kolejnym przybliżeniu zakłada się, że odchylenia od przybliżenia zerowego są małe, co umożliwia tzw. linearyzację równań, wyprowadzenie równań hydrodynamiki gazu lepkiego i uzyskanie wzorów na współczynniki przewodnictwa cieplnego, współczynniki lepkości itp. Oprócz klasycznej k.t.g. istnieje jej kwantowy odpowiednik, pozwalający (w powiązaniu z odpowiednimi, upraszczającymi założeniami) na podanie przybliżonego opisu zjawiska oporu elektr. w metalach (pochodzącego od domieszek) czy też opisu ruchu gazu elektronów i dziur w półprzewodnikach. K.t.g. stanowi dział kinetycznej teorii materii.
2> = 3kBT/m (kB — stała Boltzmanna, m — masa cząsteczki gazu, T — temperatura), która jest miarą temperatury; na każdy stopień swobody (stopnie swobody) jednej cząsteczki przypada średnio energia kBT/2 (ekwipartycji energii zasada). Gdy gaz nie jest w równowadze (postać f różni się od postaci rozkładu Maxwella) — na ogół temperatura, gęstość i średnia prędkość cząsteczek nie są stałe w całej objętości jaką zajmuje gaz. Gaz dąży do osiągnięcia równowagi przez wyrównanie wartości tych parametrów; zachodzi to za pośrednictwem lokalnych przekazów energii, masy i pędu (transport). Mechanizmem prowadzącym do takich przekazów w rozrzedzonym gazie są zderzenia binarne cząsteczek. Średnia droga pojedynczej cząsteczki między dwoma kolejnymi zderzeniami nosi nazwę drogi swobodnej. Dla gazu nierównowagowego znajdującego się blisko stanu równowagi przyjmuje się, że w zerowym przybliżeniu rozkład Maxwella jest spełniony lokalnie, tzn. układ jest scharakteryzowany przez lokalną temperaturę (zależną od położenia cząsteczek i czasu). Pozwala to na wyprowadzenie równań hydrodynamiki dla przepływu gazu bez uwzględnienia lepkości. W kolejnym przybliżeniu zakłada się, że odchylenia od przybliżenia zerowego są małe, co umożliwia tzw. linearyzację równań, wyprowadzenie równań hydrodynamiki gazu lepkiego i uzyskanie wzorów na współczynniki przewodnictwa cieplnego, współczynniki lepkości itp. Oprócz klasycznej k.t.g. istnieje jej kwantowy odpowiednik, pozwalający (w powiązaniu z odpowiednimi, upraszczającymi założeniami) na podanie przybliżonego opisu zjawiska oporu elektr. w metalach (pochodzącego od domieszek) czy też opisu ruchu gazu elektronów i dziur w półprzewodnikach. K.t.g. stanowi dział kinetycznej teorii materii.
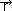 ,
, 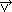 , t), gdzie f(
, t), gdzie f(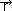 ,
, 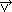 , t)d3rd3v jest liczbą cząsteczek, które w chwili t znajdują się w małym elemencie objętości przestrzeni fazowej d3rd3v wokół punktu (
, t)d3rd3v jest liczbą cząsteczek, które w chwili t znajdują się w małym elemencie objętości przestrzeni fazowej d3rd3v wokół punktu (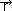 ,
, 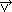 ). Czasową ewolucję funkcji rozkładu opisuje kinetyczne równanie Boltzmanna. Dla gazu w stanie równowagi termodynamicznej f przyjmuje postać rozkładu Maxwella. Znajomość f pozwala obliczać wszystkie wielkości termodynamiczne, np.: średni kwadrat prędkości cząsteczek <
). Czasową ewolucję funkcji rozkładu opisuje kinetyczne równanie Boltzmanna. Dla gazu w stanie równowagi termodynamicznej f przyjmuje postać rozkładu Maxwella. Znajomość f pozwala obliczać wszystkie wielkości termodynamiczne, np.: średni kwadrat prędkości cząsteczek <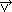 2> = 3kBT/m (kB — stała Boltzmanna, m — masa cząsteczki gazu, T — temperatura), która jest miarą temperatury; na każdy stopień swobody (stopnie swobody) jednej cząsteczki przypada średnio energia kBT/2 (ekwipartycji energii zasada). Gdy gaz nie jest w równowadze (postać f różni się od postaci rozkładu Maxwella) — na ogół temperatura, gęstość i średnia prędkość cząsteczek nie są stałe w całej objętości jaką zajmuje gaz. Gaz dąży do osiągnięcia równowagi przez wyrównanie wartości tych parametrów; zachodzi to za pośrednictwem lokalnych przekazów energii, masy i pędu (transport). Mechanizmem prowadzącym do takich przekazów w rozrzedzonym gazie są zderzenia binarne cząsteczek. Średnia droga pojedynczej cząsteczki między dwoma kolejnymi zderzeniami nosi nazwę drogi swobodnej. Dla gazu nierównowagowego znajdującego się blisko stanu równowagi przyjmuje się, że w zerowym przybliżeniu rozkład Maxwella jest spełniony lokalnie, tzn. układ jest scharakteryzowany przez lokalną temperaturę (zależną od położenia cząsteczek i czasu). Pozwala to na wyprowadzenie równań hydrodynamiki dla przepływu gazu bez uwzględnienia lepkości. W kolejnym przybliżeniu zakłada się, że odchylenia od przybliżenia zerowego są małe, co umożliwia tzw. linearyzację równań, wyprowadzenie równań hydrodynamiki gazu lepkiego i uzyskanie wzorów na współczynniki przewodnictwa cieplnego, współczynniki lepkości itp. Oprócz klasycznej k.t.g. istnieje jej kwantowy odpowiednik, pozwalający (w powiązaniu z odpowiednimi, upraszczającymi założeniami) na podanie przybliżonego opisu zjawiska oporu elektr. w metalach (pochodzącego od domieszek) czy też opisu ruchu gazu elektronów i dziur w półprzewodnikach. K.t.g. stanowi dział kinetycznej teorii materii.
2> = 3kBT/m (kB — stała Boltzmanna, m — masa cząsteczki gazu, T — temperatura), która jest miarą temperatury; na każdy stopień swobody (stopnie swobody) jednej cząsteczki przypada średnio energia kBT/2 (ekwipartycji energii zasada). Gdy gaz nie jest w równowadze (postać f różni się od postaci rozkładu Maxwella) — na ogół temperatura, gęstość i średnia prędkość cząsteczek nie są stałe w całej objętości jaką zajmuje gaz. Gaz dąży do osiągnięcia równowagi przez wyrównanie wartości tych parametrów; zachodzi to za pośrednictwem lokalnych przekazów energii, masy i pędu (transport). Mechanizmem prowadzącym do takich przekazów w rozrzedzonym gazie są zderzenia binarne cząsteczek. Średnia droga pojedynczej cząsteczki między dwoma kolejnymi zderzeniami nosi nazwę drogi swobodnej. Dla gazu nierównowagowego znajdującego się blisko stanu równowagi przyjmuje się, że w zerowym przybliżeniu rozkład Maxwella jest spełniony lokalnie, tzn. układ jest scharakteryzowany przez lokalną temperaturę (zależną od położenia cząsteczek i czasu). Pozwala to na wyprowadzenie równań hydrodynamiki dla przepływu gazu bez uwzględnienia lepkości. W kolejnym przybliżeniu zakłada się, że odchylenia od przybliżenia zerowego są małe, co umożliwia tzw. linearyzację równań, wyprowadzenie równań hydrodynamiki gazu lepkiego i uzyskanie wzorów na współczynniki przewodnictwa cieplnego, współczynniki lepkości itp. Oprócz klasycznej k.t.g. istnieje jej kwantowy odpowiednik, pozwalający (w powiązaniu z odpowiednimi, upraszczającymi założeniami) na podanie przybliżonego opisu zjawiska oporu elektr. w metalach (pochodzącego od domieszek) czy też opisu ruchu gazu elektronów i dziur w półprzewodnikach. K.t.g. stanowi dział kinetycznej teorii materii.Krzysztof Rościszewski


