skończenie wymiarowa
Encyklopedia PWN
dział analizy mat., poświęcony abstrakcyjnym uogólnieniom znanych pojęć geometrii klas. i matematyki elementarnej: długości odcinka, pola wielokąta, objętości wielościanu, 0-wymiarowej miary liczącej, tzn. liczby elementów zbioru.
mat. grupa jednoznacznie wyznaczona przez skończony zbiór elementów generujących r1,r2,... ,rn i relacje określające: 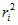 = e,
= e, 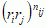 , gdzie 2 ≤ nij ≤ ∞;
, gdzie 2 ≤ nij ≤ ∞;
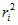 = e,
= e, 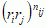 , gdzie 2 ≤ nij ≤ ∞;
, gdzie 2 ≤ nij ≤ ∞;
mat. nieujemna liczba rzeczywista r przypisana przestrzeni metrycznej X wg następującej procedury: 1) dla liczb rzeczywistych p ≥ 0 i d > 0 rozpatruje się pokrycia przestrzeni X kulami o środkach w punktach xi ∈ X i średnicach di ≤ d, i = 1, 2, ... (dopuszcza się również skończoną liczbę kul), 2) znajduje się kres dolny md liczb 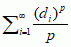 po wszystkich takich pokryciach i wylicza granicę
po wszystkich takich pokryciach i wylicza granicę 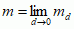 (m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).
(m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).
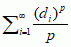 po wszystkich takich pokryciach i wylicza granicę
po wszystkich takich pokryciach i wylicza granicę 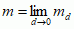 (m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).
(m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).
mat. miara zbudowana na wzór geom., standardowych: długości, pola, objętości (miara);
mat. jedno z podstawowych pojęć algebry liniowej; funkcję f z przestrzeni liniowej V w przestrzeń liniową W, f: V → W, gdzie V i W są przestrzeniami liniowymi nad tym samym ciałem K, nazywa się p.l., jeżeli zachodzi równość f(λx + μy) = λf(x) + μf(y) dla dowolnych λ, μ ∈ K i x, y ∈ V.


