jest przeprowadzana w filtrze elektrycznym. Filtracja może dotyczyć sygnałów ciągłych bądź dyskretnych i przebiegać w dziedzinie czasu lub częstotliwości. Przykładem filtracji jest oddzielanie sygnału użytecznego od szumu czy wygładzanie przebiegów elektrycznych. Mechanizmami filtracji zajmuje się teoria filtracji; umożliwia ona obliczanie parametrów i konstruowanie filtrów elektr. przeznaczonych do konkretnego zastosowania. Najbardziej rozwinięta jest teoria filtracji liniowej. Przebieg filtracji zależy od charakterystyki filtru. Właściwości filtru liniowego w dziedzinie czasu najczęściej określa tzw.
odpowiedź impulsowa h(
t) (dla procesu ciągłego) lub
h(
n) (dla procesu dyskretnego), opisująca postać sygnału na wyjściu filtru, na którego wejście podano impuls Diraca (pojedynczy impuls o nieskończonej amplitudzie i czasie trwania równym 0). Filtracja sygnału w dziedzinie czasu, tj. zależność między sygnałem wejściowym
x(
t) a sygnałem wyjściowym
y(
t) filtru jest opisana dla procesu ciągłego iloczynem splotowym (
splot funkcji):
y(
t) =
x(
t)*
h(
t), przedstawianym w postaci całki:
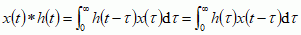
;
dla procesu dyskretnego iloczyn splotowy ma postać sumy:
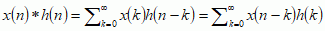 .
. Przebieg filtracji sygnału w dziedzinie częst. określa się za pomocą
charakterystyki częstotliwościowej filtru, zw. również
charakterystyką widmową; dostarcza ona informacji, jak są przenoszone przez filtr sygnały o określonych częstotliwościach. Charakterystykę tę można otrzymać wyznaczając
transmitancję operatorową filtru
H(
s) (dla procesu ciągłego) lub
H(
z) (dla procesu dyskretnego); ma ona postać przekształcenia całkowego Laplace’a (
transformata) odpowiedzi impulsowej
h(
t). Proces filtracji w dziedzinie częst. jest opisany zwykłym iloczynem transformaty sygnału wejściowego oraz transmitancji operatorowej układu filtrującego, np. dla sygnałów ciągłych iloczynem:
Y(
s) =
H(
s)
X(
s), gdzie
Y(
s) i
X(
s) są transformatami Laplace’a odpowiednio sygnału wyjściowego i wejściowego filtru. W wypadku sygnałów dyskretnych obowiązuje podobny wzór:
Y(
z) =
H(
z)
X(
z), w którym
z jest częst. zespoloną w transformacji Laurenta. W wypadku filtrów zbudowanych z rezystorów, cewek, kondensatorów i źródeł sterowanych transmitancja ma postać funkcji (wymiernej) zmiennej zespolonej
s, tj.
H(
s) =
L(
s)/
M(
s), gdzie
L(
s) i
M(
s) są wielomianami o stałych współczynnikach, przy czym przyjmuje się
s = j
ω (
ω = 2π
f jest pulsacją,
f — częst., a j =

— jednostką urojoną); w postaci wykładniczej
H(
s) =
H(j
ω) = |H(j
ω)|e
jφ (ω). Wielkość |
H(j
ω)| jest modułem transmitancji i jej przebieg w zależności od pulsacji (częst.) nosi nazwę
charakterystyki amplitudowej, natomiast przebieg
φ(
ω) (
φ — faza sygnału) —
charakterystyki fazowej. Przy dużych zmianach wartości modułu wygodnie jest wprowadzić charakterystyki logarytmiczne; zmiany przedstawia się wówczas najczęściej w postaci: 20 log
10|
H(j
ω)| i wyraża w decybelach (dB).
W większości zastosowań wystarcza rozważenie procesu filtracji w dziedzinie częst., co znacznie upraszcza wszystkie operacje matematyczne. Filtracja sygnałów w dziedzinie czasu jest zagadnieniem bardziej złożonym teoretycznie i stosuje się ją gł. w wypadku przetwarzania sygnałów stochastycznych (będących losowymi funkcjami czasu). W większości przypadków nie istnieje wówczas analityczne rozwiązanie problemu. Podstawą teorii filtracji w dziedzinie czasu, rozwiniętej przez N. Wienera, A. Kołmogorowa i R. Kalmana, jest założenie, że przetwarzane sygnały stanowią pewne procesy stochastyczne, w których opisie wykorzystuje się narzędzia statystyki, nie zaś charakterystyki częstotliwościowe. To podejście wiąże się z
teorią estymacji.
Filtracja jest istotną operacją przetwarzania sygnałów. Jest stosowana powszechnie w odbiornikach radiowych i telewizyjnych, w systemach regulacji automatycznej, w modelowaniu obiektów dynamicznych, a także w metodach prognozowania i estymacji procesów. Filtracja w dziedzinie czasu jest stosowana m.in. przy określaniu orbit sztucznych satelitów Ziemi, śledzeniu ruchu samolotów lub sterowaniu torem pocisków.
Pionierami teorii filtracji byli matematycy A.M. Legendre i C.F. Gauss, a jej wielkimi współcz. twórcami — Wiener, G. Campbell, Kalman i Kołmogorow.
Stanisław Osowski
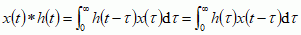 ;
;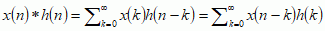 .
.  — jednostką urojoną); w postaci wykładniczej H(s) = H(jω) = |H(jω)|ejφ (ω). Wielkość |H(jω)| jest modułem transmitancji i jej przebieg w zależności od pulsacji (częst.) nosi nazwę charakterystyki amplitudowej, natomiast przebieg φ(ω) (φ — faza sygnału) — charakterystyki fazowej. Przy dużych zmianach wartości modułu wygodnie jest wprowadzić charakterystyki logarytmiczne; zmiany przedstawia się wówczas najczęściej w postaci: 20 log10|H(jω)| i wyraża w decybelach (dB).
— jednostką urojoną); w postaci wykładniczej H(s) = H(jω) = |H(jω)|ejφ (ω). Wielkość |H(jω)| jest modułem transmitancji i jej przebieg w zależności od pulsacji (częst.) nosi nazwę charakterystyki amplitudowej, natomiast przebieg φ(ω) (φ — faza sygnału) — charakterystyki fazowej. Przy dużych zmianach wartości modułu wygodnie jest wprowadzić charakterystyki logarytmiczne; zmiany przedstawia się wówczas najczęściej w postaci: 20 log10|H(jω)| i wyraża w decybelach (dB).