Hooke’a prawo,
podstawowe prawo liniowej teorii sprężystości;
Hooke’a prawo
Encyklopedia PWN
podaje liniową zależność między naprężeniami i odkształceniem ciała sprężystego przy odkształceniach nie przekraczających granicy proporcjonalności. Przy rozciąganiu (ściskaniu) jednoosiowym (jednoosiowy stan naprężeń) p.H. ma postać σ = Eε, gdzie σ oznacza naprężenie normalne, ε — odkształcenie, E — moduł Younga (moduł sprężystości podłużnej); w przypadku pręta długości L, rozciąganego lub ściskanego siłą podłużną F, p.H. wyraża się wzorem ΔL = FL/Es (gdzie ΔL — wydłużenie bezwzględne pręta, s — pole przekroju poprzecznego) lub wzorem ε = σ/E (gdzie σ = F/s — naprężenie, ε = ΔL/L — względne wydłużenie pręta). Przy odkształceniach postaciowych (ścinanie, skręcanie) p.H. wyraża się wzorem τ = Gγ, gdzie τ — naprężenie styczne, γ — kąt odkształcenia postaciowego, G — moduł Kirchhoffa (moduł sprężystości poprzecznej). 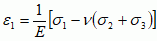
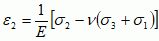
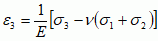
Uogólnione p.H. wynika z zasady superpozycji, która mówi, że suma skutków wywołanych w danym punkcie ciała przez poszczególne przyczyny jest równa skutkowi wywołanemu w tym punkcie przez sumę przyczyn. Przy rozciąganiu (ściskaniu) trójosiowym (trójosiowy stan naprężeń), określonym za pomocą sześciu składowych naprężenia, uogólnione p.H. mówi, że każda z sześciu składowych stanu naprężenia σij w dowolnym punkcie ciała jest liniową funkcją sześciu składowych εkl stanu odkształcenia w tym punkcie, czyli σij = Cijkl · εkl, gdzie Cijkl — współczynniki sprężystości. Gdy stan naprężenia jest określony za pomocą naprężeń gł. σ1, σ2, σ3 i odkształceń gł. ε1, ε2, ε3, wówczas uogólnione p.H. wyraża się wzorami:
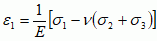
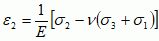
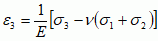
gdzie ν — współczynnik Poissona. Dla odkształceń postaciowych pozostają w mocy równości typu τ = Gγ. P.H. podał 1660 R. Hooke, a uogólnił je 1822 A. Cauchy.


