tensorem metrycznym
Encyklopedia PWN
mat. symetryczny tensor 2. rzędu (zwykle oznaczany gμν), opisujący odległości między bliskimi punktami w przestrzeni lub czasoprzestrzeni: ds2 = gμνdxμdxν = g00dx0dx0 + g01dx0dx1 + ... + gnndxndxn.
geometrie Riemanna, geometrie riemannowskie,
wielowymiarowe uogólnienia klas. geometrii różniczkowej na dwuwymiarowych powierzchniach (zapoczątkowanej przez C.F. Gaussa), właśc. teoria przestrzeni Riemanna, stworzona 1854 przez B. Riemanna.
mat. symbole określone dla danej kwadratowej formy różniczkowej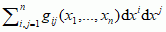 
przedstawiające wyrażenia: 1)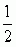 
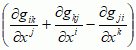, gdzie i, j, k = 1, ... , n — s.Ch. pierwszego rodzaju, oznaczane Γij,k lub 
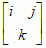; 2)
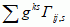, gdzie macierz [gks] jest macierzą odwrotną do [gij] — s.Ch. drugiego rodzaju, oznaczane 
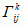lub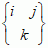 
;
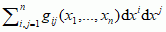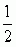
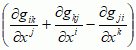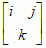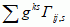przedstawiające wyrażenia: 1) , gdzie i, j, k = 1, ... , n — s.Ch. pierwszego rodzaju, oznaczane Γij,k lub ; 2), gdzie macierz [gks] jest macierzą odwrotną do [gij] — s.Ch. drugiego rodzaju, oznaczane 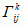lub ;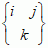
geometria
dyscyplina nauki zajmująca się badaniem figur, tj. fragmentów rozmaitych przestrzeni.
[gr. gḗ ‘ziemia’, metréō ‘mierzę’],
mat. rozmaitość różniczkowa (rozmaitość) wyposażona w tensor metryki riemannowskiej, tzn. iloczyn skalarny w przestrzeni stycznej (ściśle: gładki przekrój wiązki dwuliniowych dodatnio określonych form symetrycznych na przestrzeni stycznej);
