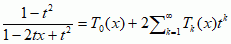wielomiany Czebyszewa

wielomiany Czebyszewa,

mat. wielomiany postaci T_n(x) = cos(n arc cos x), gdzie n = 0, 1, 2, ... (n-ty w.Cz. pierwszego rodzaju) i U_n(x) = 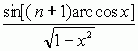(n-ty w.Cz. drugiego rodzaju).

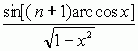Kilka początkowych w.Cz.: T₀(x) = 1, T₁(x) = x, T₂(x) = 2x² − 1, T₃(x) = 4x³ − 3x; U₀(x) = 1, U₁(x) = 2x, U₂(x) = 4x² − 1, U₃(x) = 8x³ − 4x. Między w.Cz. pierwszego i drugiego rodzaju zachodzi związek U_n(x) = .

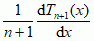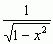Wielomiany T_n tworzą w przedziale [–1, 1] układ ortogonalny z wagą , tzn. zachodzą następujące związki 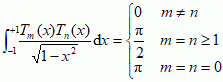. Spełniają równość rekurencyjną T_{n + 1}(x) = 2xT_n(x) − T_{n −1}(x) oraz następujące równanie różniczkowe zwyczajne: (1 − x²)T_n″(x) − xT_n′(x) + n²T(x) = 0.

W.Cz. można również definiować jako współczynniki rozwinięcia w szereg Taylora odpowiednich funkcji względem parametru t, np.:

Badał je 1748 L. Euler w związku z rozkładem funkcji cosnx wg potęg cosx, a następnie 1854 P. Czebyszew w związku z zagadnieniami teorii aproksymacji. W.Cz. — jako aproksymacje funkcji ciągłych — znajdują zastosowanie w wielu gałęziach matematyki i techniki.