statystyczne testy,
procedury weryfikacji hipotez statystycznych;
statystyczne testy
Encyklopedia PWN
do weryfikacji parametrycznych hipotez zerowych (H0) są używane testy istotności (np. test (t) — Studenta), podczas gdy weryfikacje hipotez nieparametrycznych opieramy na testach zgodności (np. test chi-kwadrat (χ2).
Stosowane testy (istotności lub zgodności) są zmiennymi losowymi postaci standaryzowanej o znanych rozkładach teoretycznych (np. test istotności t ma rozkład Studenta, natomiast test zgodności χ2 ma rozkład Pearsona), z reguły całkowicie określonych przez liczbę stopni swobody. Krytyczne poziomy tych testów mogą być ustalane na podstawie 2 źródeł: z tablic statystycznych (odczyty mniej dokładnie i z ograniczeniami) lub z komputerowego kalkulatora prawdopodobieństwa (odczyty bardziej dokładne i bez ograniczeń). Przy założeniu prawdziwości H0 i na deklarowanym wcześniej poziomie istotności α (zazwyczaj z przedziału od 0,01 do 0,10) są wskazywane liczbowe przedziały odrzuceń H0, lokalizowane dwustronnie lub jednostronnie (co zależy od kierunku hipotezy alternatywnej H1). Po sprawdzeniu, gdzie mieści się liczbowa wartość obliczonego testu statystycznego, jest podejmowana — na deklarowanym poziomie α — jedna z 2 możliwych decyzji weryfikacyjnych, mianowicie: albo odrzucenie H0, gdy poziom testu znajduje się w przedziale krytycznym (wtedy wyniki z prób losowych różnią się istotnie od założeń), albo też nieodrzucenie H0, gdy poziom testu znajduje się poza przedziałem krytycznym (wtedy wyniki z prób losowych różnią się nieistotnie od założeń).
Decyzje weryfikacyjne mają różną moc (są ostre, czyli jednoznaczne lub rozmyte, czyli niejednoznaczne). Stopień ostrości podejmowanych decyzji weryfikacji H0 można ustalić przez porównanie deklarowanego (α) oraz krytycznego (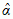 ) poziomu istotności. Przyjmuje się konwencję, że przy weryfikacji hipotez zerowych testami istotności lub zgodności, podejmowane decyzje są ostre (jednoznaczne) wtedy, kiedy:
) poziomu istotności. Przyjmuje się konwencję, że przy weryfikacji hipotez zerowych testami istotności lub zgodności, podejmowane decyzje są ostre (jednoznaczne) wtedy, kiedy: 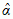 < 0,01 w przypadku odrzucenia H0, lub wtedy, kiedy
< 0,01 w przypadku odrzucenia H0, lub wtedy, kiedy 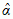 > 0,10 w przypadku nieodrzucenia H0. Oferta testów bardziej specjalistycznych jest niezwykle szeroka, a ich stosowanie ułatwiają komputerowe pakiety statystyczno-graficzne (np. STATISTICA PL, wersja 6). Problematyce tej jest także poświęcona bogata literatura przedmiotu.
> 0,10 w przypadku nieodrzucenia H0. Oferta testów bardziej specjalistycznych jest niezwykle szeroka, a ich stosowanie ułatwiają komputerowe pakiety statystyczno-graficzne (np. STATISTICA PL, wersja 6). Problematyce tej jest także poświęcona bogata literatura przedmiotu.
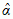 ) poziomu istotności. Przyjmuje się konwencję, że przy weryfikacji hipotez zerowych testami istotności lub zgodności, podejmowane decyzje są ostre (jednoznaczne) wtedy, kiedy:
) poziomu istotności. Przyjmuje się konwencję, że przy weryfikacji hipotez zerowych testami istotności lub zgodności, podejmowane decyzje są ostre (jednoznaczne) wtedy, kiedy: 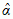 < 0,01 w przypadku odrzucenia H0, lub wtedy, kiedy
< 0,01 w przypadku odrzucenia H0, lub wtedy, kiedy 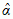 > 0,10 w przypadku nieodrzucenia H0. Oferta testów bardziej specjalistycznych jest niezwykle szeroka, a ich stosowanie ułatwiają komputerowe pakiety statystyczno-graficzne (np. STATISTICA PL, wersja 6). Problematyce tej jest także poświęcona bogata literatura przedmiotu.
> 0,10 w przypadku nieodrzucenia H0. Oferta testów bardziej specjalistycznych jest niezwykle szeroka, a ich stosowanie ułatwiają komputerowe pakiety statystyczno-graficzne (np. STATISTICA PL, wersja 6). Problematyce tej jest także poświęcona bogata literatura przedmiotu.Andrzej Luszniewicz


