współczynnikami wielomianu
Encyklopedia PWN
mat. suma jednomianów; dokładniej — wielomian n zmiennych x1, ... , xn o współczynnikach z przemiennego pierścienia R (np. ciała) jest sumą wyrażeń postaci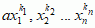 
ze współczynnikami a ∈ R, a ≠ 0.
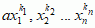ze współczynnikami a ∈ R, a ≠ 0.
mat. wielomiany postaci Tn(x) = cos(n arc cos x), gdzie n = 0, 1, 2, ... (n-ty w.Cz. pierwszego rodzaju) i Un(x) =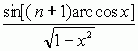 
(n-ty w.Cz. drugiego rodzaju).
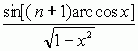(n-ty w.Cz. drugiego rodzaju).
algebry twierdzenie podstawowe, zasadnicze twierdzenie algebry,
mat. twierdzenie o istnieniu dla każdego wielomianu f(z) = anzn + ... + a1z + a0 stopnia n > 0, o współczynnikach zespolonych (liczby zespolone) takiej liczby zespolonej ξ, zw. pierwiastkiem wielomianu f, że f(ξ) = 0.
;
mat. pojęcie algebraiczne najczęściej definiowane dla pierścieni, rzadziej dla innych algebr ogólnych (np. dla półgrup).
mat. pewne klasy funkcji często występujące przy rozwiązywaniu rozmaitych zagadnień fizyki, matematyki i techniki, w szczególności przy rozwiązywaniu równań różniczkowych cząstkowych metodą rozdzielania zmiennych;
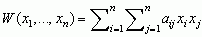