mimośród stożkowej,
mat. wielkość e w równaniu stożkowej we współrzędnych biegunowych: r = p/(1 − e cos φ), gdzie biegun układu pokrywa się z ogniskiem stożkowej, oś biegunowa jest zawarta w osi symetrii stożkowej przechodzącej przez jej ognisko, a p jest liczbą zwaną parametrem stożkowej;
mimośród stożkowej
Encyklopedia PWN
wartość e jest ściśle związana z rodzajem stożkowej, i tak: dla okręgu e = 0, dla elipsy e ∈ (0, 1), dla paraboli e = 1, dla hiperboli e > 1. Dla elipsy opisanej równaniem x2/a2 + y2/b2 = 1 mimośród 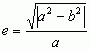 ; dla hiperboli opisanej równaniem x2/a2– y2/b2 = 1 mimośród
; dla hiperboli opisanej równaniem x2/a2– y2/b2 = 1 mimośród 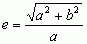 . Mimośród stożkowej można także określić jako stosunek odległości jej dowolnego punktu od ogniska i pewnej prostej zwanej kierownicą.
. Mimośród stożkowej można także określić jako stosunek odległości jej dowolnego punktu od ogniska i pewnej prostej zwanej kierownicą.
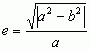 ; dla hiperboli opisanej równaniem x2/a2– y2/b2 = 1 mimośród
; dla hiperboli opisanej równaniem x2/a2– y2/b2 = 1 mimośród 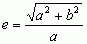 . Mimośród stożkowej można także określić jako stosunek odległości jej dowolnego punktu od ogniska i pewnej prostej zwanej kierownicą.
. Mimośród stożkowej można także określić jako stosunek odległości jej dowolnego punktu od ogniska i pewnej prostej zwanej kierownicą. 

