gradient

gradient

[łac.],

mat. operator różniczkowy zdefiniowany następująco: g. funkcji skalarnej φ(x, y, z) jest wektor o składowych ∂φ/∂x, ∂φ/∂y, ∂φ/∂z, oznaczony symbolem grad lub ∇ (nabla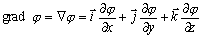): , gdzie 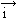, , 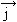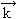są wektorami jednostkowymi prostokątnego układu współrzędnych kartezjańskich (analogicznie definiuje się g. skalarnej funkcji większej liczby zmiennych).

Wektor gradφ w danym punkcie P charakteryzuje zachowanie się funkcji φ (x, y, z) w tym punkcie, określając kierunek i szybkość największego jej wzrostu. Na przykład, jeśli funkcja φ (x, y, z) oznacza potencjał pola elektrostatycznego lub pole rozkładu temperatury, to gradφ obliczony w danym punkcie wskazuje kierunek, w którym potencjał lub temperatura doznaje najszybszego wzrostu (w porównaniu z innymi kierunkami przechodzącymi przez dany punkt), a także szybkość tego wzrostu. Kierunek wektora gradφ w danym punkcie jest prostopadły do powierzchni równych wartości φ (x, y, z) = const (powierzchni ekwipotencjalnej), przechodzącej przez ten punkt.