Taylora wzór,
mat. jeden z najważniejszych wzorów rachunku różniczkowego, odkryty 1712 przez B. Taylora;
Taylora wzór
Encyklopedia PWN
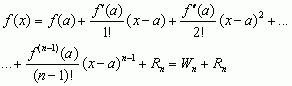
, gdzie tzw. reszta najczęściej jest przedstawiana w postaci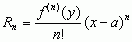 
, przy czym liczba y leży między a i x, zależy od x, n, f, a funkcja f ma ciągłe pochodne do rzędu n – 1 w przedziale [a, b] oraz skończoną pochodną f (n)(x) w przedziale (a, b); wielomian Taylora Wn przybliża funkcję f, co wykorzystuje się często we wzorach przybliżonych i asymptotycznych; istnieje również analogiczny wzór Taylora dla funkcji wielu zmiennych; jeżeli a = 0, to wzór Taylora nosi nazwę wzoru Maclaurina i ma postać:
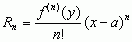, przy czym liczba y leży między a i x, zależy od x, n, f, a funkcja f ma ciągłe pochodne do rzędu n – 1 w przedziale [a, b] oraz skończoną pochodną f (n)(x) w przedziale (a, b); wielomian Taylora Wn przybliża funkcję f, co wykorzystuje się często we wzorach przybliżonych i asymptotycznych; istnieje również analogiczny wzór Taylora dla funkcji wielu zmiennych; jeżeli a = 0, to wzór Taylora nosi nazwę wzoru Maclaurina i ma postać: 
.
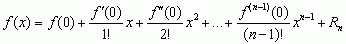