szeregiem Maclaurina
Encyklopedia PWN
mat. szereg potęgowy postaci f(0) + f ′(0)/1! · x + ... + f (n)(0)/n! · xn + ...;
mat. wzór wyrażający funkcję wielokrotnie różniczkowalną w otoczeniu punktu x = 0 za pomocą sumy pewnego wielomianu (suma częściowa szeregu Maclaurina) i tzw. reszty;
mat. jedno z najważniejszych pojęć analizy matematycznej, pozwalające w pewnych sytuacjach nadać ścisły sens dodawaniu nieskończonej liczby składników;
szereg dwumianowy, szereg dwumienny,
mat. szereg potęgowy będący rozwinięciem funkcji (1 + x)α w szereg Taylora (Maclaurina), α — dowolna liczba rzeczywista;
mat. szereg potęgowy (szereg) postaci: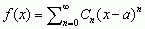 
, gdzie cn = f (n)(a)/n!, który powstaje ze wzoru Taylora, gdy reszta Rn dąży do zera przy n → ∞;
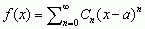, gdzie cn = f (n)(a)/n!, który powstaje ze wzoru Taylora, gdy reszta Rn dąży do zera przy n → ∞;
mat. przedstawienie danej funkcji f — o wartościach rzeczywistych bądź zespolonych, lub ogólniej, o wartościach z przestrzeni wektorowej unormowanej (przestrzeń unormowana), np. n-wymiarowej przestrzeni kartezjańskiej, przestrzeni Banacha, przestrzeni Hilberta — w postaci sumy szeregu funkcyjnego (szereg): f(x) =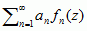 
, gdzie an są współczynnikami, fn zaś funkcjami, na ogół prostszej natury niż sama funkcja f;
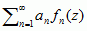, gdzie an są współczynnikami, fn zaś funkcjami, na ogół prostszej natury niż sama funkcja f;
