trysekcja kąta,
mat. zagadnienie konstrukcyjne podziału dowolnego kąta na 3 równe części.
trysekcja kąta
Encyklopedia PWN
Zagadnienie to (wraz z delijskim problemem i kwadraturą koła) rozważane było już przez matematyków starogreckich, którzy początkowo próbowali rozwiązać je za pomocą cyrkla i linijki, co prowadziło do pozytywnego wyniku jedynie dla kątów postaci 90°/n (n = 1, 2, 3,...); później (ok. V w.) próbowano rozwiązać je za pomocą innych środków konstrukcyjnych, np. wykorzystując kwadratrysę, konchoidę; Archimedes np. zaproponował następujący sposób trysekcji kąta 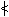 ABC = 3α za pomocą cyrkla i linijki z podziałką: promieniem BA (równym np. jedności) zakreśla się okrąg (otrzymując punkty A i C), przedłuża średnicę AD poza okrąg i tak się umieszcza linijkę z zaznaczonym na niej odcinkiem EF = AB, by przechodziła ona przez punkt C oraz by zaznaczony na niej punkt F leżał na okręgu, punkt E zaś na przedłużeniu średnicy AD; wówczas
ABC = 3α za pomocą cyrkla i linijki z podziałką: promieniem BA (równym np. jedności) zakreśla się okrąg (otrzymując punkty A i C), przedłuża średnicę AD poza okrąg i tak się umieszcza linijkę z zaznaczonym na niej odcinkiem EF = AB, by przechodziła ona przez punkt C oraz by zaznaczony na niej punkt F leżał na okręgu, punkt E zaś na przedłużeniu średnicy AD; wówczas 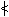 DEF = 1/3
DEF = 1/3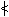 ABC. W średniowieczu stwierdzono, że zagadnienie trysekcji kąta prowadzi do rozwiązania równania algebraicznego stopnia trzeciego postaci x3 – 3x – 2cos 3α = 0, którego pierwiastek x = EB konstruuje się następnie za pomocą rozmaitych środków konstrukcyjnych (dla pewnych kątów α wystarczy w tym celu cyrkiel i linijka; niemożność trysekcji kąta za pomocą cyrkla i linijki udowodnił (1837) matematyk francuski L.P. Wantzel.
ABC. W średniowieczu stwierdzono, że zagadnienie trysekcji kąta prowadzi do rozwiązania równania algebraicznego stopnia trzeciego postaci x3 – 3x – 2cos 3α = 0, którego pierwiastek x = EB konstruuje się następnie za pomocą rozmaitych środków konstrukcyjnych (dla pewnych kątów α wystarczy w tym celu cyrkiel i linijka; niemożność trysekcji kąta za pomocą cyrkla i linijki udowodnił (1837) matematyk francuski L.P. Wantzel.
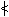 ABC = 3α za pomocą cyrkla i linijki z podziałką: promieniem BA (równym np. jedności) zakreśla się okrąg (otrzymując punkty A i C), przedłuża średnicę AD poza okrąg i tak się umieszcza linijkę z zaznaczonym na niej odcinkiem EF = AB, by przechodziła ona przez punkt C oraz by zaznaczony na niej punkt F leżał na okręgu, punkt E zaś na przedłużeniu średnicy AD; wówczas
ABC = 3α za pomocą cyrkla i linijki z podziałką: promieniem BA (równym np. jedności) zakreśla się okrąg (otrzymując punkty A i C), przedłuża średnicę AD poza okrąg i tak się umieszcza linijkę z zaznaczonym na niej odcinkiem EF = AB, by przechodziła ona przez punkt C oraz by zaznaczony na niej punkt F leżał na okręgu, punkt E zaś na przedłużeniu średnicy AD; wówczas 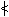 DEF = 1/3
DEF = 1/3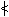 ABC. W średniowieczu stwierdzono, że zagadnienie trysekcji kąta prowadzi do rozwiązania równania algebraicznego stopnia trzeciego postaci x3 – 3x – 2cos 3α = 0, którego pierwiastek x = EB konstruuje się następnie za pomocą rozmaitych środków konstrukcyjnych (dla pewnych kątów α wystarczy w tym celu cyrkiel i linijka; niemożność trysekcji kąta za pomocą cyrkla i linijki udowodnił (1837) matematyk francuski L.P. Wantzel.
ABC. W średniowieczu stwierdzono, że zagadnienie trysekcji kąta prowadzi do rozwiązania równania algebraicznego stopnia trzeciego postaci x3 – 3x – 2cos 3α = 0, którego pierwiastek x = EB konstruuje się następnie za pomocą rozmaitych środków konstrukcyjnych (dla pewnych kątów α wystarczy w tym celu cyrkiel i linijka; niemożność trysekcji kąta za pomocą cyrkla i linijki udowodnił (1837) matematyk francuski L.P. Wantzel. 

