delijski problem, problem podwojenia sześcianu,
mat. jedno z klasycznych zagadnień konstrukcyjnych, polegające na zbudowaniu sześcianu o objętości 2 razy większej niż sześcian dany, pochodzące od starożytnych Greków;
delijski problem
Encyklopedia PWN
problem delijski sprowadza się do konstrukcji odcinka długości 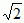 przy danym odcinku długości 1. Problem ten zajmował matematyków przez wiele stuleci; w efekcie istnieją konstrukcje przybliżone, a także konstrukcje wykorzystujące dodatkowo pewne krzywe, np. konstrukcja Dioklesa wykorzystująca cysoidę, konstrukcja Nikomedesa wykorzystująca konchoidę. Rozwiązanie problemu delijskiego jest niewykonalne za pomocą cyrkla i linijki — pierwszy dowód tego faktu podał P.L. Wantzel (1837). Problem delijski pochodzi od starożytnych Greków (VI w. p.n.e.); według legendy wyrocznia na wyspie Delos poradziła, by dla powstrzymania panującej tam zarazy dwukrotnie powiększyć ołtarz ofiarny, nie zmieniając jego kształtu.
przy danym odcinku długości 1. Problem ten zajmował matematyków przez wiele stuleci; w efekcie istnieją konstrukcje przybliżone, a także konstrukcje wykorzystujące dodatkowo pewne krzywe, np. konstrukcja Dioklesa wykorzystująca cysoidę, konstrukcja Nikomedesa wykorzystująca konchoidę. Rozwiązanie problemu delijskiego jest niewykonalne za pomocą cyrkla i linijki — pierwszy dowód tego faktu podał P.L. Wantzel (1837). Problem delijski pochodzi od starożytnych Greków (VI w. p.n.e.); według legendy wyrocznia na wyspie Delos poradziła, by dla powstrzymania panującej tam zarazy dwukrotnie powiększyć ołtarz ofiarny, nie zmieniając jego kształtu.
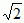 przy danym odcinku długości 1. Problem ten zajmował matematyków przez wiele stuleci; w efekcie istnieją konstrukcje przybliżone, a także konstrukcje wykorzystujące dodatkowo pewne krzywe, np. konstrukcja Dioklesa wykorzystująca cysoidę, konstrukcja Nikomedesa wykorzystująca konchoidę. Rozwiązanie problemu delijskiego jest niewykonalne za pomocą cyrkla i linijki — pierwszy dowód tego faktu podał P.L. Wantzel (1837). Problem delijski pochodzi od starożytnych Greków (VI w. p.n.e.); według legendy wyrocznia na wyspie Delos poradziła, by dla powstrzymania panującej tam zarazy dwukrotnie powiększyć ołtarz ofiarny, nie zmieniając jego kształtu.
przy danym odcinku długości 1. Problem ten zajmował matematyków przez wiele stuleci; w efekcie istnieją konstrukcje przybliżone, a także konstrukcje wykorzystujące dodatkowo pewne krzywe, np. konstrukcja Dioklesa wykorzystująca cysoidę, konstrukcja Nikomedesa wykorzystująca konchoidę. Rozwiązanie problemu delijskiego jest niewykonalne za pomocą cyrkla i linijki — pierwszy dowód tego faktu podał P.L. Wantzel (1837). Problem delijski pochodzi od starożytnych Greków (VI w. p.n.e.); według legendy wyrocznia na wyspie Delos poradziła, by dla powstrzymania panującej tam zarazy dwukrotnie powiększyć ołtarz ofiarny, nie zmieniając jego kształtu. 

