płaszczyzna

płaszczyzna,

mat. jedno z podstawowych pojęć geometrii, uważane za pojęcie pierwotne;

własności płaszczyzny w przestrzeni trójwymiarowej (euklidesowej) są scharakteryzowane przez aksjomaty, np. 1) przez 3 punkty niewspółliniowe przechodzi tylko jedna płaszczyzna; 2) płaszczyzna dzieli przestrzeń na 2 części, tzw. półprzestrzenie, przy czym: a) w każdej z tych części leży dowolnie wiele punktów, b) odcinek łączący 2 punkty położone w tej samej półprzestrzeni nie przecina płaszczyzny dzielącej, c) odcinek łączący 2 punkty położone w różnych półprzestrzeniach przecina płaszczyznę dzielącą; 3) 2 różne płaszczyzny mające wspólny punkt mają też wspólną prostą (krawędź przecięcia tych płaszczyzn). W geometrii analitycznej płaszczyzna jest określona równaniem liniowym ax + by + cz + d = 0 (gdzie przynajmniej jedna z liczb a, b, c jest różna od 0), w którym współczynniki a, b, c są składowymi wektora prostopadłego do płaszczyzny; 2 płaszczyzny a_ix + b_iy + c_iz  + d_i = 0 (i = 1, 2) są równoległe, gdy a₁/a₂ = b₁/b₂ = c₁/c₂, natomiast są prostopadłe gdy a₁ · a₂ + b₁ · b₂ + c₁ · c₂ = 0; odległość punktu (x₀, y₀, z₀) od płaszczyzny wyraża się wzorem |ax₀ + by₀ + cz₀ + d| /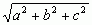.
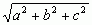