Euklides, Eukleídēs, żył na przeł. IV i III w. p.n.e.,
grecki matematyk.
Żył na przełomie IV i III w. p.n.e.
Prawie nic nie wiadomo o jego życiu. Prawdopodobnie studiował w Akademii Platońskiej w Atenach. Wiadomo, że nauczał w Aleksandrii za rządów Ptolemeusza I. Sławę wielkiego uczonego zawdzięcza swemu głównemu dziełu Stoicheía geōmetrías (w tłumaczeniu polskim Elementy), w którym usystematyzował ówczesną wiedzę matematyczną w postaci aksjomatycznego wykładu. Dzieło to po wynalezieniu druku miało ponad tysiąc wydań i wywarło ogromny wpływ na rozwój nauki. Z przekładów łacińskich są znane też 2 dzieła geometryczne: Data, zawierające ćwiczenia do Elementów, i De divisionibus, o podziale figury na daną liczbę równych części, a także 2 dzieła dotyczące optyki: Catoptrica i Optica (Euklides sformułował prawo załamania się światła oraz zasadę prostoliniowego rozchodzenia się promieni świetlnych), Phaenomena z astronomii i jedno z zakresu teorii muzyki Sectio canonis. Pozostałe dzieła Euklidesa są znane jedynie z ich omówienia u Pappusa.
Elementy
Dzieło to przetrwało do naszych czasów w całości, najstarsze zachowane rękopisy są jednak o kilka wieków późniejsze od oryginału. Łączy ono w jedną całość dokonania wcześniejszych matematyków greckich, m.in. Talesa, Pitagorasa, Eudoksosa, Teajteta, Archytasa. Jest w nim też oryginalny wkład samego Euklidesa. Jednak szczególne znaczenie ma przede wszystkim sposób zebrania materiału w całość. Euklides zastosował w Elementach po raz pierwszy metodę aksjomatyczną — sformułował listę założeń (podstawowych twierdzeń, pewników lub, jak je sam nazywał, postulatów), z których następnie wyprowadzał na drodze logicznego rozumowania wszystkie twierdzenia.
W 13 księgach zostały objęte następujące zagadnienia: I — podstawy planimetrii, II — arytmetyka geometryczna, III — okrąg i koło, IV — wielokąty, V — teoria proporcji wielkości geometrycznych Eudoksosa, VI — podobieństwo figur, VII — geometryczna teoria liczb, VIII — proporcje ciągłe, IX — rozkład na czynniki pierwsze (algorytm Euklidesa), X — teoria niewymierności kwadratowych Teajteta, XI — podstawy stereometrii, XII — podobieństwo brył, XIII — wielościany foremne. Niektóre wydania zawierają księgi XIV i XV — dodane przez późniejszych komentatorów. Pierwszego polskiego przekładu Elementów (8 ksiąg, z angielskiego) dokonał 1807 J. Czech: Euklidesa początków jeometrii Xiąg ośmioro, to jest sześć pierwszych, jedenasta i dwunasta z dodanymi przypisami i trygonometrią dla pożytku młodzi akademickiej tłumaczone i wydane. Od 2005 jest realizowany w Polsce projekt badawczy „Księgi Euklidesa” (www.interklasa.pl/euklides).
Rola Elementów w rozwoju nauki była olbrzymia. Dzieło to przez wieki stanowiło wzór dla nauk ścisłych. Uzupełniano w nim luki, rozwijano niektóre działy, badano znaczenie postulatów, m.in. bezowocne próby wyprowadzenia postulatu V (postulatu równoległości) z pozostałych aksjomatów doprowadziły do powstania geometrii nieeuklidesowych. Prawdopodobnie była to, po Biblii, najczęściej studiowana, tłumaczona i wydawana drukiem książka w dziejach.
Elementy stały się modelem aksjomatyczno-dedukcyjnego ujmowania wiedzy, gdzie najpierw wymaga się jasnego przedstawienia założeń w postaci pojęć pierwotnych (nie definiowanych) i aksjomatów, a następnie ścisłego dowodzenia wynikających z nich konkluzji, które nazywamy twierdzeniami lub wnioskami. Było podstawowym podręcznikiem matematyki, w niektórych krajach jeszcze w XX w.
Postulat równoległości Euklidesa
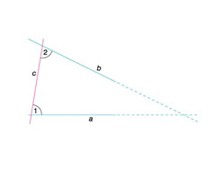
Ostatni z pięciu postulatów podanych przez Euklidesa w pierwszej księdze jego Elementów głosi: jeśli na płaszczyźnie prosta c, przecinająca dwie inne proste a i b, tworzy z nimi kąty wewnętrzne (1 i 2 na rysunku) o sumie mniejszej od 2 kątów prostych (tzn. 180°), to proste a i b przecinają się po tej samej stronie c, po której leżą te kąty. W powszechnie obecnie przyjętym sformułowaniu postulat równoległości Euklidesa brzmi: jeżeli aoznacza dowolną prostą, A — dowolny punkt nie leżący na a, to w płaszczyźnie wyznaczonej przez a i cA istnieje co najwyżej jedna prosta przechodząca przez A i nie przecinająca a. Postulat ten jest istotny dla geometrii euklidesowej. Jego zaprzeczenie prowadzi do geometrii nieeuklidesowych.