macierz S, macierz rozpraszania,
macierz nieskończonego wymiaru, której elementy określają amplitudy prawdopodobieństwa przejścia ze stanu początkowego (opisującego stan układu w chwili −∞) do stanu końcowego (w chwili +∞);
macierz S
Encyklopedia PWN
odgrywa ona podstawową rolę w opisie procesów rozpraszania w teorii cząstek elementarnych i teorii jądra atomowego. Macierz rozpraszania spełnia następujące warunki: 1) unitarność: SS+ = S+S = 1, będąca konsekwencją zachowania prawdopodobieństwa (gdzie S+ = 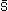 T— macierz sprzężona hermitowsko); 2) niezmienniczość ze względu na transformacje grupy Poincarégo (szczególne transformacje Lorentza, przesunięcia w czasie i przestrzeni); 3) niezmienniczość ze względu na transformacje cechowania elektromagnet. U(1) i silnego SU(3); 4) niezmienniczość ze względu na transformację CPT (superpozycja sprzężenia ładunkowego, parzystości przestrzennej i odwrócenia czasu). Z unitarności m. S wypływa ważny wniosek zw. twierdzeniem optycznym, zgodnie z którym amplituda elastycznego rozpraszania 2 cząstek a i b „do przodu” (czyli pod kątem θ = 0°) jest proporcjonalna do całkowitego przekroju czynnego na rozpraszanie a i b oraz do wartości bezwzględnej pędu zderzających się cząstek w układzie środka masy. Unitarność m. S pozwala np. na oszacowanie górnej granicy masy (MH) cząstek Higgsa. Rachunek zaburzeń w kwantowej teorii pola formułuje się, korzystając z możliwości przedstawienia macierzy rozpraszania w postaci nieskończonego szeregu perturbacyjnego. Mimo bardzo dobrej zgodności danych doświadczalnych (dotyczących np. oddziaływań elektromagnetycznych) z przewidywaniami teoret. uwzględniającymi jedynie kilka pierwszych wyrazów szeregu perturbacyjnego, nie istnieje dowód zbieżności szeregu nawet dla elektrodynamiki kwantowej.
T— macierz sprzężona hermitowsko); 2) niezmienniczość ze względu na transformacje grupy Poincarégo (szczególne transformacje Lorentza, przesunięcia w czasie i przestrzeni); 3) niezmienniczość ze względu na transformacje cechowania elektromagnet. U(1) i silnego SU(3); 4) niezmienniczość ze względu na transformację CPT (superpozycja sprzężenia ładunkowego, parzystości przestrzennej i odwrócenia czasu). Z unitarności m. S wypływa ważny wniosek zw. twierdzeniem optycznym, zgodnie z którym amplituda elastycznego rozpraszania 2 cząstek a i b „do przodu” (czyli pod kątem θ = 0°) jest proporcjonalna do całkowitego przekroju czynnego na rozpraszanie a i b oraz do wartości bezwzględnej pędu zderzających się cząstek w układzie środka masy. Unitarność m. S pozwala np. na oszacowanie górnej granicy masy (MH) cząstek Higgsa. Rachunek zaburzeń w kwantowej teorii pola formułuje się, korzystając z możliwości przedstawienia macierzy rozpraszania w postaci nieskończonego szeregu perturbacyjnego. Mimo bardzo dobrej zgodności danych doświadczalnych (dotyczących np. oddziaływań elektromagnetycznych) z przewidywaniami teoret. uwzględniającymi jedynie kilka pierwszych wyrazów szeregu perturbacyjnego, nie istnieje dowód zbieżności szeregu nawet dla elektrodynamiki kwantowej.
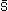 T— macierz sprzężona hermitowsko); 2) niezmienniczość ze względu na transformacje grupy Poincarégo (szczególne transformacje Lorentza, przesunięcia w czasie i przestrzeni); 3) niezmienniczość ze względu na transformacje cechowania elektromagnet. U(1) i silnego SU(3); 4) niezmienniczość ze względu na transformację CPT (superpozycja sprzężenia ładunkowego, parzystości przestrzennej i odwrócenia czasu). Z unitarności m. S wypływa ważny wniosek zw. twierdzeniem optycznym, zgodnie z którym amplituda elastycznego rozpraszania 2 cząstek a i b „do przodu” (czyli pod kątem θ = 0°) jest proporcjonalna do całkowitego przekroju czynnego na rozpraszanie a i b oraz do wartości bezwzględnej pędu zderzających się cząstek w układzie środka masy. Unitarność m. S pozwala np. na oszacowanie górnej granicy masy (MH) cząstek Higgsa. Rachunek zaburzeń w kwantowej teorii pola formułuje się, korzystając z możliwości przedstawienia macierzy rozpraszania w postaci nieskończonego szeregu perturbacyjnego. Mimo bardzo dobrej zgodności danych doświadczalnych (dotyczących np. oddziaływań elektromagnetycznych) z przewidywaniami teoret. uwzględniającymi jedynie kilka pierwszych wyrazów szeregu perturbacyjnego, nie istnieje dowód zbieżności szeregu nawet dla elektrodynamiki kwantowej.
T— macierz sprzężona hermitowsko); 2) niezmienniczość ze względu na transformacje grupy Poincarégo (szczególne transformacje Lorentza, przesunięcia w czasie i przestrzeni); 3) niezmienniczość ze względu na transformacje cechowania elektromagnet. U(1) i silnego SU(3); 4) niezmienniczość ze względu na transformację CPT (superpozycja sprzężenia ładunkowego, parzystości przestrzennej i odwrócenia czasu). Z unitarności m. S wypływa ważny wniosek zw. twierdzeniem optycznym, zgodnie z którym amplituda elastycznego rozpraszania 2 cząstek a i b „do przodu” (czyli pod kątem θ = 0°) jest proporcjonalna do całkowitego przekroju czynnego na rozpraszanie a i b oraz do wartości bezwzględnej pędu zderzających się cząstek w układzie środka masy. Unitarność m. S pozwala np. na oszacowanie górnej granicy masy (MH) cząstek Higgsa. Rachunek zaburzeń w kwantowej teorii pola formułuje się, korzystając z możliwości przedstawienia macierzy rozpraszania w postaci nieskończonego szeregu perturbacyjnego. Mimo bardzo dobrej zgodności danych doświadczalnych (dotyczących np. oddziaływań elektromagnetycznych) z przewidywaniami teoret. uwzględniającymi jedynie kilka pierwszych wyrazów szeregu perturbacyjnego, nie istnieje dowód zbieżności szeregu nawet dla elektrodynamiki kwantowej. 

