Ornsteina–Uhlenbecka proces

Ornsteina–Uhlenbecka proces

[p. ornstina ulenbeka],

mat., fiz. stacjonarne rozwiązanie stochastycznego równania różniczkowego m dV_t = −βV_tdt + dW_t (równanie Langevina) — V_t jest prędkością drobiny o masie m zawieszonej w ośrodku (cieczy lub gazie), β odpowiada współczynnikowi tarcia w ośrodku, natomiast dW_t jest wpływem zderzeń z cząsteczkami ośrodka (czyli różniczką, w sensie Ito, ruchu Browna);

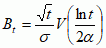p.O.–U. jest jednorodnym w czasie procesem Markowa, a zarazem procesem gaussowskim, o zerowej funkcji średnich, w którym funkcja kowariancji jest dana wzorem B(t, s) = E(V_tV_s) = σ²e^{–\alpha\,|t-s|}, przy czym α = β/m; wiele własności p.O.–U., w tym jego „markows-kość”, można wyprowadzić z faktu, że proces B_t = jest standardowym procesem Wienera; m.in. wynika stąd, że prawie wszystkie trajektorie p.O.–U. są nigdzie nieróżniczkowalnymi funkcjami ciągłymi, tak samo jak dla procesu Wienera.