Naviera–Stokesa równanie ruchu płynów

Naviera–Stokesa równanie ruchu płynów

[r. r. p. n. sto^uksa],

podstawowe równanie ruchu płynów lepkich newtonowskich; wg tego równania, zgodnie z II zasadą dynamiki (Newtona zasady dynamiki), przyspieszenie jednostkowej masy płynu jest równe sumie sił działających na tę masę, tzn. siły masowej (np. grawitacyjnej, siły bezwładności), siły ciśnieniowej (2. człon równania), siły tarcia wewn. pochodzącej od naprężeń ścinających przy deformacji płynu (człon 3. i 4. równania);

dla płynów nieściśliwych ma postać: , gdzie: 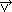— prędkość płynu, t — czas, ρ — gęstość, p — ciśnienie, 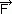— jednostkowa siła masowa, ν — lepkość kinematyczna; człon ν△ (△ — laplasjan) obrazuje działające w płynie siły lepkości; podstawowe równanie opisujące przepływy płynu — laminarne i turbulentne (przy założeniu, że płyn jest ośrodkiem ciągłym).