równania różniczkowe zwyczajne,
równania zawierające niewiadomą funkcję y = y(x) jednej zmiennej x, jej pochodne y(k)(x) różnych rzędów, jak też zmienną niezależną x;
równania różniczkowe zwyczajne
Encyklopedia PWN
rzędem różniczkowego równania zwyczajnego nazywa się największy rząd występującej w nim pochodnej; różniczkowe równanie zwyczajne rzędu n można zapisać najogólniej w postaci F(x, y, y′, ... , y(n)) = 0, gdzie F jest funkcją n + 2 zmiennych x, y, y′, ... , y(n), określoną i ciągłą w pewnym obszarze (n + 2)-wymiarowym, i gdzie y(k) oznacza pochodną rzędu k; 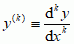 . Rozwiązaniem lub całką różniczkowego równania zwyczajnego nazywa się każdą funkcję y = y(x), która tożsamościowo spełnia to równanie; wykres funkcji y = y(x) nazywa się w tym przypadku krzywą całkową lub krócej całką różniczkowego równania zwyczajnego; rozwiązać lub scałkować różniczkowe równanie zwyczajne znaczy znaleźć wszystkie jego całki; np. wszystkie całki różniczkowych równań zwyczajnych pierwszego rzędu xy′ + 3x – 2y = 0 można przedstawić za pomocą wzoru y(x, C) = Cx2 + 3x; istnieje więc cała rodzina całek zależna w tym przypadku od jednego parametru C (tzw. stałej całkowania); podobnie wszystkie całki różniczkowego równania zwyczajnego drugiego rzędu xy″ + y′ = 0 obejmuje wzór y(x, A, B) = A ln|x| + B, gdzie A i B oznaczają dowolne stałe; rozwiązanie ogólne różniczkowego równania zwyczajnego F(x, y, y′, ... , y(n)) = 0 rzędu n ma postać y = y(x, C1, C2, .... , Cn), zależy więc od n dowolnych parametrów (stałych całkowania); przyjmując za te stałe konkretne liczby, otrzymuje się jedną konkretną całkę, zw. całką lub rozwiązaniem szczególnym (np. w przykładzie różniczkowego równania zwyczajnego drugiego rzędu dla A = 1, B = 0 otrzymuje się rozwiązanie szczególne y = ln|x|); wybieranie konkretnych wartości na stałe całkowania wiąże się z pewnymi żądaniami natury geom., np. z dwuparametrowej rodziny całek φ(x, A, B) można wybrać jedną żądając: 1) by krzywa całkowa φ(x, A, B) przechodziła przez dany punkt P(x0, y0) oraz miała w nim z góry określone nachylenie y0 — są to tzw. warunki początkowe, które z punktu widzenia dynamiki oznaczają, że w chwili początkowej jest określone położenie punktu i jego prędkość; 2) by krzywa całkowa φ(x, A, B) przechodziła przez z góry określone 2 punkty P(x1, y1) i Q(x2, y2) lub by nachylenie krzywej całkowej było w tych warunkach z góry określone — są tzw. warunki brzegowe. Dla pewnych różniczkowych równań zwyczajnych, oprócz rozwiązania ogólnego, istnieją jeszcze tzw. rozwiązania (całki) osobliwe, np. dla różniczkowego równania zwyczajnego Clairauta y – xy′ + 1/2(y′)2 = 0 całką ogólną jest jednoparametrowa rodzina prostych y = Cx – 1/2C2, a całką osobliwą krzywa y = 1/2x2 (której nie można otrzymać z rozwiązania ogólnego żadnym doborem stałej C); krzywa ta jest tzw. obwiednią danej rodziny prostych.
. Rozwiązaniem lub całką różniczkowego równania zwyczajnego nazywa się każdą funkcję y = y(x), która tożsamościowo spełnia to równanie; wykres funkcji y = y(x) nazywa się w tym przypadku krzywą całkową lub krócej całką różniczkowego równania zwyczajnego; rozwiązać lub scałkować różniczkowe równanie zwyczajne znaczy znaleźć wszystkie jego całki; np. wszystkie całki różniczkowych równań zwyczajnych pierwszego rzędu xy′ + 3x – 2y = 0 można przedstawić za pomocą wzoru y(x, C) = Cx2 + 3x; istnieje więc cała rodzina całek zależna w tym przypadku od jednego parametru C (tzw. stałej całkowania); podobnie wszystkie całki różniczkowego równania zwyczajnego drugiego rzędu xy″ + y′ = 0 obejmuje wzór y(x, A, B) = A ln|x| + B, gdzie A i B oznaczają dowolne stałe; rozwiązanie ogólne różniczkowego równania zwyczajnego F(x, y, y′, ... , y(n)) = 0 rzędu n ma postać y = y(x, C1, C2, .... , Cn), zależy więc od n dowolnych parametrów (stałych całkowania); przyjmując za te stałe konkretne liczby, otrzymuje się jedną konkretną całkę, zw. całką lub rozwiązaniem szczególnym (np. w przykładzie różniczkowego równania zwyczajnego drugiego rzędu dla A = 1, B = 0 otrzymuje się rozwiązanie szczególne y = ln|x|); wybieranie konkretnych wartości na stałe całkowania wiąże się z pewnymi żądaniami natury geom., np. z dwuparametrowej rodziny całek φ(x, A, B) można wybrać jedną żądając: 1) by krzywa całkowa φ(x, A, B) przechodziła przez dany punkt P(x0, y0) oraz miała w nim z góry określone nachylenie y0 — są to tzw. warunki początkowe, które z punktu widzenia dynamiki oznaczają, że w chwili początkowej jest określone położenie punktu i jego prędkość; 2) by krzywa całkowa φ(x, A, B) przechodziła przez z góry określone 2 punkty P(x1, y1) i Q(x2, y2) lub by nachylenie krzywej całkowej było w tych warunkach z góry określone — są tzw. warunki brzegowe. Dla pewnych różniczkowych równań zwyczajnych, oprócz rozwiązania ogólnego, istnieją jeszcze tzw. rozwiązania (całki) osobliwe, np. dla różniczkowego równania zwyczajnego Clairauta y – xy′ + 1/2(y′)2 = 0 całką ogólną jest jednoparametrowa rodzina prostych y = Cx – 1/2C2, a całką osobliwą krzywa y = 1/2x2 (której nie można otrzymać z rozwiązania ogólnego żadnym doborem stałej C); krzywa ta jest tzw. obwiednią danej rodziny prostych.
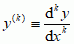 . Rozwiązaniem lub całką różniczkowego równania zwyczajnego nazywa się każdą funkcję y = y(x), która tożsamościowo spełnia to równanie; wykres funkcji y = y(x) nazywa się w tym przypadku krzywą całkową lub krócej całką różniczkowego równania zwyczajnego; rozwiązać lub scałkować różniczkowe równanie zwyczajne znaczy znaleźć wszystkie jego całki; np. wszystkie całki różniczkowych równań zwyczajnych pierwszego rzędu xy′ + 3x – 2y = 0 można przedstawić za pomocą wzoru y(x, C) = Cx2 + 3x; istnieje więc cała rodzina całek zależna w tym przypadku od jednego parametru C (tzw. stałej całkowania); podobnie wszystkie całki różniczkowego równania zwyczajnego drugiego rzędu xy″ + y′ = 0 obejmuje wzór y(x, A, B) = A ln|x| + B, gdzie A i B oznaczają dowolne stałe; rozwiązanie ogólne różniczkowego równania zwyczajnego F(x, y, y′, ... , y(n)) = 0 rzędu n ma postać y = y(x, C1, C2, .... , Cn), zależy więc od n dowolnych parametrów (stałych całkowania); przyjmując za te stałe konkretne liczby, otrzymuje się jedną konkretną całkę, zw. całką lub rozwiązaniem szczególnym (np. w przykładzie różniczkowego równania zwyczajnego drugiego rzędu dla A = 1, B = 0 otrzymuje się rozwiązanie szczególne y = ln|x|); wybieranie konkretnych wartości na stałe całkowania wiąże się z pewnymi żądaniami natury geom., np. z dwuparametrowej rodziny całek φ(x, A, B) można wybrać jedną żądając: 1) by krzywa całkowa φ(x, A, B) przechodziła przez dany punkt P(x0, y0) oraz miała w nim z góry określone nachylenie y0 — są to tzw. warunki początkowe, które z punktu widzenia dynamiki oznaczają, że w chwili początkowej jest określone położenie punktu i jego prędkość; 2) by krzywa całkowa φ(x, A, B) przechodziła przez z góry określone 2 punkty P(x1, y1) i Q(x2, y2) lub by nachylenie krzywej całkowej było w tych warunkach z góry określone — są tzw. warunki brzegowe. Dla pewnych różniczkowych równań zwyczajnych, oprócz rozwiązania ogólnego, istnieją jeszcze tzw. rozwiązania (całki) osobliwe, np. dla różniczkowego równania zwyczajnego Clairauta y – xy′ + 1/2(y′)2 = 0 całką ogólną jest jednoparametrowa rodzina prostych y = Cx – 1/2C2, a całką osobliwą krzywa y = 1/2x2 (której nie można otrzymać z rozwiązania ogólnego żadnym doborem stałej C); krzywa ta jest tzw. obwiednią danej rodziny prostych.
. Rozwiązaniem lub całką różniczkowego równania zwyczajnego nazywa się każdą funkcję y = y(x), która tożsamościowo spełnia to równanie; wykres funkcji y = y(x) nazywa się w tym przypadku krzywą całkową lub krócej całką różniczkowego równania zwyczajnego; rozwiązać lub scałkować różniczkowe równanie zwyczajne znaczy znaleźć wszystkie jego całki; np. wszystkie całki różniczkowych równań zwyczajnych pierwszego rzędu xy′ + 3x – 2y = 0 można przedstawić za pomocą wzoru y(x, C) = Cx2 + 3x; istnieje więc cała rodzina całek zależna w tym przypadku od jednego parametru C (tzw. stałej całkowania); podobnie wszystkie całki różniczkowego równania zwyczajnego drugiego rzędu xy″ + y′ = 0 obejmuje wzór y(x, A, B) = A ln|x| + B, gdzie A i B oznaczają dowolne stałe; rozwiązanie ogólne różniczkowego równania zwyczajnego F(x, y, y′, ... , y(n)) = 0 rzędu n ma postać y = y(x, C1, C2, .... , Cn), zależy więc od n dowolnych parametrów (stałych całkowania); przyjmując za te stałe konkretne liczby, otrzymuje się jedną konkretną całkę, zw. całką lub rozwiązaniem szczególnym (np. w przykładzie różniczkowego równania zwyczajnego drugiego rzędu dla A = 1, B = 0 otrzymuje się rozwiązanie szczególne y = ln|x|); wybieranie konkretnych wartości na stałe całkowania wiąże się z pewnymi żądaniami natury geom., np. z dwuparametrowej rodziny całek φ(x, A, B) można wybrać jedną żądając: 1) by krzywa całkowa φ(x, A, B) przechodziła przez dany punkt P(x0, y0) oraz miała w nim z góry określone nachylenie y0 — są to tzw. warunki początkowe, które z punktu widzenia dynamiki oznaczają, że w chwili początkowej jest określone położenie punktu i jego prędkość; 2) by krzywa całkowa φ(x, A, B) przechodziła przez z góry określone 2 punkty P(x1, y1) i Q(x2, y2) lub by nachylenie krzywej całkowej było w tych warunkach z góry określone — są tzw. warunki brzegowe. Dla pewnych różniczkowych równań zwyczajnych, oprócz rozwiązania ogólnego, istnieją jeszcze tzw. rozwiązania (całki) osobliwe, np. dla różniczkowego równania zwyczajnego Clairauta y – xy′ + 1/2(y′)2 = 0 całką ogólną jest jednoparametrowa rodzina prostych y = Cx – 1/2C2, a całką osobliwą krzywa y = 1/2x2 (której nie można otrzymać z rozwiązania ogólnego żadnym doborem stałej C); krzywa ta jest tzw. obwiednią danej rodziny prostych. Różniczkowe równania zwyczajne opisują wiele zjawisk i procesów zachodzących w przyrodzie i stąd wynika ich ogromne znaczenie w naukach przyr.; np. jeżeli na punkt materialny o masie m poruszający się po osi x-ów działa siła sprężysta F proporcjonalna do wychylenia punktu z położenia równowagi O i skierowana ku O (F = –k2x), to zgodnie z drugim prawem Newtona (ma = F) m = –k2x, gdzie
= –k2x, gdzie  = d2x/dt2 oznacza przyspieszenie punktu, a x = x(t) jego wychylenie z położenia równowagi; rozwiązanie tego różniczkowego równania zwyczajnego ma postać x(t) = A cos(ωt + α0) i nazywa się równaniem ruchu harmonicznego; wśród typów różniczkowych równań zwyczajnych często spotykanych w zastosowaniach wyróżniają się różniczkowe równania zwyczajne liniowe pierwszego rzędu y′ + f(x)y = h(x) oraz drugiego rzędu y″ + f(x)y′ + g(x)y = h(x) — gdzie funkcje f, g i h są znane; gdy h(x) ≡ 0 równania te nazywają się jednorodnymi, a gdy h(x) ≢ 0 — niejednorodnymi; często występują również układy różniczkowych równań zwyczajnych, zwłaszcza pierwszego i drugiego rzędu. Początki badań nad różniczkowymi równaniami zwyczajnymi przypadają na XVII w., prawie równocześnie z powstaniem rachunku różniczkowego i całkowego; w XVIII w., gł. dzięki pracom D. Bernoulliego, J. d’Alemberta, L. Eulera, teoria różniczkowych równań zwyczajnych przekształciła się w samodzielną dyscyplinę mat. z właściwą sobie problematyką znajdującą coraz szersze zastosowania w naukach przyr., a także w technice.
= d2x/dt2 oznacza przyspieszenie punktu, a x = x(t) jego wychylenie z położenia równowagi; rozwiązanie tego różniczkowego równania zwyczajnego ma postać x(t) = A cos(ωt + α0) i nazywa się równaniem ruchu harmonicznego; wśród typów różniczkowych równań zwyczajnych często spotykanych w zastosowaniach wyróżniają się różniczkowe równania zwyczajne liniowe pierwszego rzędu y′ + f(x)y = h(x) oraz drugiego rzędu y″ + f(x)y′ + g(x)y = h(x) — gdzie funkcje f, g i h są znane; gdy h(x) ≡ 0 równania te nazywają się jednorodnymi, a gdy h(x) ≢ 0 — niejednorodnymi; często występują również układy różniczkowych równań zwyczajnych, zwłaszcza pierwszego i drugiego rzędu. Początki badań nad różniczkowymi równaniami zwyczajnymi przypadają na XVII w., prawie równocześnie z powstaniem rachunku różniczkowego i całkowego; w XVIII w., gł. dzięki pracom D. Bernoulliego, J. d’Alemberta, L. Eulera, teoria różniczkowych równań zwyczajnych przekształciła się w samodzielną dyscyplinę mat. z właściwą sobie problematyką znajdującą coraz szersze zastosowania w naukach przyr., a także w technice.
 = –k2x, gdzie
= –k2x, gdzie  = d2x/dt2 oznacza przyspieszenie punktu, a x = x(t) jego wychylenie z położenia równowagi; rozwiązanie tego różniczkowego równania zwyczajnego ma postać x(t) = A cos(ωt + α0) i nazywa się równaniem ruchu harmonicznego; wśród typów różniczkowych równań zwyczajnych często spotykanych w zastosowaniach wyróżniają się różniczkowe równania zwyczajne liniowe pierwszego rzędu y′ + f(x)y = h(x) oraz drugiego rzędu y″ + f(x)y′ + g(x)y = h(x) — gdzie funkcje f, g i h są znane; gdy h(x) ≡ 0 równania te nazywają się jednorodnymi, a gdy h(x) ≢ 0 — niejednorodnymi; często występują również układy różniczkowych równań zwyczajnych, zwłaszcza pierwszego i drugiego rzędu. Początki badań nad różniczkowymi równaniami zwyczajnymi przypadają na XVII w., prawie równocześnie z powstaniem rachunku różniczkowego i całkowego; w XVIII w., gł. dzięki pracom D. Bernoulliego, J. d’Alemberta, L. Eulera, teoria różniczkowych równań zwyczajnych przekształciła się w samodzielną dyscyplinę mat. z właściwą sobie problematyką znajdującą coraz szersze zastosowania w naukach przyr., a także w technice.
= d2x/dt2 oznacza przyspieszenie punktu, a x = x(t) jego wychylenie z położenia równowagi; rozwiązanie tego różniczkowego równania zwyczajnego ma postać x(t) = A cos(ωt + α0) i nazywa się równaniem ruchu harmonicznego; wśród typów różniczkowych równań zwyczajnych często spotykanych w zastosowaniach wyróżniają się różniczkowe równania zwyczajne liniowe pierwszego rzędu y′ + f(x)y = h(x) oraz drugiego rzędu y″ + f(x)y′ + g(x)y = h(x) — gdzie funkcje f, g i h są znane; gdy h(x) ≡ 0 równania te nazywają się jednorodnymi, a gdy h(x) ≢ 0 — niejednorodnymi; często występują również układy różniczkowych równań zwyczajnych, zwłaszcza pierwszego i drugiego rzędu. Początki badań nad różniczkowymi równaniami zwyczajnymi przypadają na XVII w., prawie równocześnie z powstaniem rachunku różniczkowego i całkowego; w XVIII w., gł. dzięki pracom D. Bernoulliego, J. d’Alemberta, L. Eulera, teoria różniczkowych równań zwyczajnych przekształciła się w samodzielną dyscyplinę mat. z właściwą sobie problematyką znajdującą coraz szersze zastosowania w naukach przyr., a także w technice.

