prosta,
mat. pojęcie pierwotne (niedefiniowane) geometrii, intuicyjnie odpowiadające najkrótszej i najmniej zakrzywionej drodze.
prosta
Encyklopedia PWN
Własności prostej są zawarte w aksjomatach geometrii elementarnej, np.: 2 punkty wyznaczają prostą, 2 przecinające się proste wyznaczają płaszczyznę; w geometrii analitycznej płaskiej prostą określa się jako zbiór punktów P(x, y), których współrzędne x, y spełniają równanie liniowe ax + by + c = 0 (równanie prostej) przy warunku, że a2 + b2 > 0; liczby a i b w ostatnim równaniu oznaczają współrzędne (składowe) wektora normalnego do prostej; równanie kierunkowe prostej ma postać y = mx + b (m = tg α — współczynnik kierunkowy prostej, α — kąt, który ta prosta tworzy z dodatnim zwrotem osi odciętych); równanie odcinkowe prostej ma postać 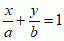 , gdzie a i b oznaczają współrzędne punktów, w których ta prosta przecina odpowiednie osie współrzędnych; w przestrzeni trójwymiarowej prostą określa się równaniem
, gdzie a i b oznaczają współrzędne punktów, w których ta prosta przecina odpowiednie osie współrzędnych; w przestrzeni trójwymiarowej prostą określa się równaniem 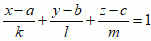 lub równaniami parametrycznymi x = kt + a, y = lt + b, z = mt + c, które oznaczają, że rozważana prosta przechodzi przez punkt P (a, b, c) i jest równoległa do wektora
lub równaniami parametrycznymi x = kt + a, y = lt + b, z = mt + c, które oznaczają, że rozważana prosta przechodzi przez punkt P (a, b, c) i jest równoległa do wektora 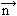 [k, l, m], parametr t zmienia się od –∞ do +∞. Uogólnieniem (odpowiednikiem) pojęcia „prostej” w geometriach innych niż euklidesowa jest geodezyjna.
[k, l, m], parametr t zmienia się od –∞ do +∞. Uogólnieniem (odpowiednikiem) pojęcia „prostej” w geometriach innych niż euklidesowa jest geodezyjna.
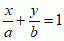 , gdzie a i b oznaczają współrzędne punktów, w których ta prosta przecina odpowiednie osie współrzędnych; w przestrzeni trójwymiarowej prostą określa się równaniem
, gdzie a i b oznaczają współrzędne punktów, w których ta prosta przecina odpowiednie osie współrzędnych; w przestrzeni trójwymiarowej prostą określa się równaniem 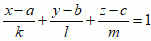 lub równaniami parametrycznymi x = kt + a, y = lt + b, z = mt + c, które oznaczają, że rozważana prosta przechodzi przez punkt P (a, b, c) i jest równoległa do wektora
lub równaniami parametrycznymi x = kt + a, y = lt + b, z = mt + c, które oznaczają, że rozważana prosta przechodzi przez punkt P (a, b, c) i jest równoległa do wektora 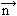 [k, l, m], parametr t zmienia się od –∞ do +∞. Uogólnieniem (odpowiednikiem) pojęcia „prostej” w geometriach innych niż euklidesowa jest geodezyjna.
[k, l, m], parametr t zmienia się od –∞ do +∞. Uogólnieniem (odpowiednikiem) pojęcia „prostej” w geometriach innych niż euklidesowa jest geodezyjna. 

