pierwiastek,
mat. pojęcie z zakresu arytmetyki i algebry.
pierwiastek
Encyklopedia PWN
1) Pierwiastkiem arytmetycznym stopnia n (n = 1, 2, 3,...) z liczby rzeczywistej nieujemnej a (a ≥ 0) nazywa się taką nieujemną liczbę rzeczywistą x (x ≥ 0), która podniesiona do potęgi n daje liczbę a (xn = a) i zapisuje się to w postaci x = 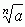 (a — liczba podpierwiastkowa); dla n = 2 pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza
(a — liczba podpierwiastkowa); dla n = 2 pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza 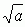 ,
, 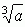 zaś nazywa się pierwiastkiem sześciennym; zachodzą reguły:
zaś nazywa się pierwiastkiem sześciennym; zachodzą reguły: 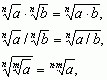
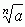 (a — liczba podpierwiastkowa); dla n = 2 pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza
(a — liczba podpierwiastkowa); dla n = 2 pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza 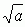 ,
, 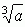 zaś nazywa się pierwiastkiem sześciennym; zachodzą reguły:
zaś nazywa się pierwiastkiem sześciennym; zachodzą reguły: 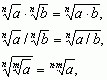
jeśli a < b, to 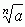 <
< 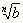 . Dla liczb rzeczywistych ujemnych (a < 0) pierwiastek stopnia nieparzystego n można sensownie określić wzorem:
. Dla liczb rzeczywistych ujemnych (a < 0) pierwiastek stopnia nieparzystego n można sensownie określić wzorem: 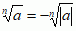 , np.
, np. 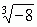 = –2;
= –2;
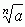 <
< 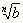 . Dla liczb rzeczywistych ujemnych (a < 0) pierwiastek stopnia nieparzystego n można sensownie określić wzorem:
. Dla liczb rzeczywistych ujemnych (a < 0) pierwiastek stopnia nieparzystego n można sensownie określić wzorem: 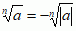 , np.
, np. 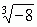 = –2;
= –2;
2) pierwiastkiem stopnia n z liczby zespolonej z = r (cos φ + i sin φ) nazywa się każdą liczbę ω, która podniesiona do potęgi n-tej daje liczbę z (ωn = z lub 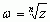 ); gdy z ≠ 0, to pierwiastków tych jest dokładnie n — wszystkie te pierwiastki otrzymuje się ze wzoru
); gdy z ≠ 0, to pierwiastków tych jest dokładnie n — wszystkie te pierwiastki otrzymuje się ze wzoru
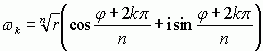 ; podstawiając tu kolejno k = 0, 1, 2, ... , n –1 otrzymuje się n różnych pierwiastków.
; podstawiając tu kolejno k = 0, 1, 2, ... , n –1 otrzymuje się n różnych pierwiastków.
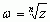 ); gdy z ≠ 0, to pierwiastków tych jest dokładnie n — wszystkie te pierwiastki otrzymuje się ze wzoru
); gdy z ≠ 0, to pierwiastków tych jest dokładnie n — wszystkie te pierwiastki otrzymuje się ze wzoru 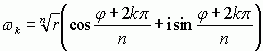 ; podstawiając tu kolejno k = 0, 1, 2, ... , n –1 otrzymuje się n różnych pierwiastków.
; podstawiając tu kolejno k = 0, 1, 2, ... , n –1 otrzymuje się n różnych pierwiastków. 

