nierówność Jensena

nierówność Jensena,

mat. nierówność wyrażająca warunek wypukłości funkcji: mówi się, że funkcja f, określona w pewnym przedziale [a, b], spełnia w tym przedziale n.J., gdy dla dowolnych punktów x, y przedziału [a, b] i dla dowolnej liczby t ∈ [0, 1] zachodzi warunek f((1 – t)x + ty) ≤ (1 – t)f(x) + tf(y), który oznacza, że wszystkie punkty łuku wykresu zawartego między punktami P(x, f(x)) i Q(y, f(y)) leżą poniżej odcinka siecznej PQ lub na tym odcinku.

Aby funkcja f spełniała n.J. w przedziale [a, b], wystarczy, by jej druga pochodna f″ była nieujemna we wszystkich punktach tego przedziału. Konsekwencją n.J. jest warunek ogólniejszy (również nazywany n.J.):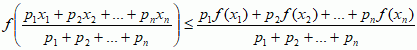

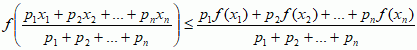
gdzie p_i są dowolnymi liczbami dodatnimi (i = 1, ... , n), a x_i — dowolnymi punktami przedziału [a, b]. Dla różnych f można z tego warunku otrzymać konkretne ważne nierówności, np. gdy f(x) = e^x, a p₁ = p₂ = ... = p_n = 1/n, to warunek ten zmienia się w nierówność między średnią geom. i średnią arytmetyczną liczb .