rachunek różnicowy, rachunek różnic skończonych,
dział matematyki zapoczątkowany przez I. Newtona znajdujący szerokie zastosowanie w metodach obliczeniowych (numerycznych) związanych z układaniem tablic mat., rozwiązywaniem przybliżonym równań algebraicznych, całkowych, różniczkowych, różniczkowo-całkowych, różnicowych, z aproksymacją itp.
rachunek różnicowy
Encyklopedia PWN
Podstawowym pojęciem rachunku różnicowego jest pojęcie różnic skończonych (zwykłych, dzielonych, wstecznych, centralnych, średnich), mianowicie: jeśli yi oznacza wartość funkcji y = f(x) w punkcie xi = x0 + ih (x0 — dowolnie obrany punkt początkowy, h — dowolny tzw. krok), to pierwszą różnicę zwykłą Δyi określa się jako przyrost 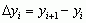 ; ogólnie k-tą różnicę zwykłą określa się jako przyrost różnic o rząd niższych:
; ogólnie k-tą różnicę zwykłą określa się jako przyrost różnic o rząd niższych: 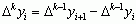 (k = 1, 2, ...), przy czym
(k = 1, 2, ...), przy czym 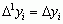 oraz
oraz 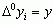 ; związek tych różnic z pochodnymi przedstawia wzór asymptotyczny:
; związek tych różnic z pochodnymi przedstawia wzór asymptotyczny: 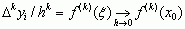 , gdzie xi < ξ < xi + k, co pozwala np. przybliżać równania różniczkowe równaniami różnicowymi (rekurencyjnymi), dającymi się już rozwiązać sposobami elementarnymi. Analogiem wzoru Taylora w rachunku różniczkowym jest następujący wzór w rachunku różnicowym:
, gdzie xi < ξ < xi + k, co pozwala np. przybliżać równania różniczkowe równaniami różnicowymi (rekurencyjnymi), dającymi się już rozwiązać sposobami elementarnymi. Analogiem wzoru Taylora w rachunku różniczkowym jest następujący wzór w rachunku różnicowym:
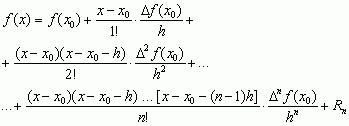 ,
,
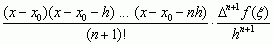 , przy czym x0 < ξ < x0 + nh.
, przy czym x0 < ξ < x0 + nh.
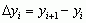 ; ogólnie k-tą różnicę zwykłą określa się jako przyrost różnic o rząd niższych:
; ogólnie k-tą różnicę zwykłą określa się jako przyrost różnic o rząd niższych: 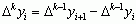 (k = 1, 2, ...), przy czym
(k = 1, 2, ...), przy czym 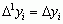 oraz
oraz 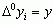 ; związek tych różnic z pochodnymi przedstawia wzór asymptotyczny:
; związek tych różnic z pochodnymi przedstawia wzór asymptotyczny: 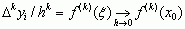 , gdzie xi < ξ < xi + k, co pozwala np. przybliżać równania różniczkowe równaniami różnicowymi (rekurencyjnymi), dającymi się już rozwiązać sposobami elementarnymi. Analogiem wzoru Taylora w rachunku różniczkowym jest następujący wzór w rachunku różnicowym:
, gdzie xi < ξ < xi + k, co pozwala np. przybliżać równania różniczkowe równaniami różnicowymi (rekurencyjnymi), dającymi się już rozwiązać sposobami elementarnymi. Analogiem wzoru Taylora w rachunku różniczkowym jest następujący wzór w rachunku różnicowym: 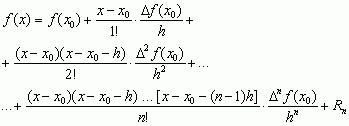 ,
, gdzie Rn wynosi:
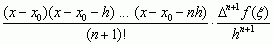 , przy czym x0 < ξ < x0 + nh.
, przy czym x0 < ξ < x0 + nh. 

