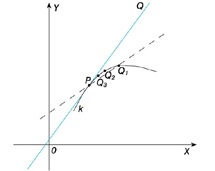
styczna,
mat. dla danej krzywej i jej punktu P — prosta, która jest granicznym położeniem siecznych tej krzywej przechodzących przez punkt P (drugi punkt przecięcia siecznej z krzywą zbliża się do punktu P).
styczna
Encyklopedia PWN
Jeśli krzywa płaska jest dana równaniem y = f(x) i w punkcie x0 istnieje pochodna funkcji f, to w tym punkcie (dokładniej w punkcie P(x0, f(x0)) krzywa ma styczną opisaną równaniem y − f(x0) = f′(x0)(x − x0). Styczną do funkcji f na płaszczyźnie w punkcie P można określić jako prostą przechodzącą przez ten punkt i której współczynnik kierunkowy jest równy pochodnej tej funkcji w zadanym punkcie. Nie każda ciągła krzywa posiada styczną w każdym punkcie, np. krzywa zadana równaniem y = |x| nie ma stycznej w punkcie (0, 0). Istnieją krzywe ciągłe, które nie mają stycznej w żadnym punkcie; jeśli w przestrzeni krzywa jest zadana przez równania parametryczne r(t) = (x(t), y(t), z(t)), to styczna w punkcie (x0, y0, z0) jest opisana równaniami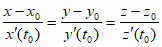 
, gdzie x0 = x(t0), y0 = y(t0), z0 = z(t0).
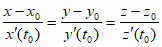, gdzie x0 = x(t0), y0 = y(t0), z0 = z(t0). 
