forma hermitowska,
mat. odwzorowanie f: X × X →  (gdzie X jest przestrzenią liniową nad ciałem liczb zespolonych
(gdzie X jest przestrzenią liniową nad ciałem liczb zespolonych  ), które jest liniowe ze względu na pierwszą zmienną i spełnia warunek:
), które jest liniowe ze względu na pierwszą zmienną i spełnia warunek: 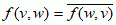 dla wszystkich v, w ∈ X;
dla wszystkich v, w ∈ X;
 (gdzie X jest przestrzenią liniową nad ciałem liczb zespolonych
(gdzie X jest przestrzenią liniową nad ciałem liczb zespolonych  ), które jest liniowe ze względu na pierwszą zmienną i spełnia warunek:
), które jest liniowe ze względu na pierwszą zmienną i spełnia warunek: 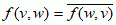 dla wszystkich v, w ∈ X;
dla wszystkich v, w ∈ X;
 n f.h. jest np.
n f.h. jest np. 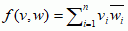 ; macierz f.h. f, tzn. macierz (f(vi,vj))1≤i,j≤n, gdzie v1, v2, ... , vn stanowią bazę X, jest macierzą hermitowską; f.h. można definiować ogólniej, zastępując ciało
; macierz f.h. f, tzn. macierz (f(vi,vj))1≤i,j≤n, gdzie v1, v2, ... , vn stanowią bazę X, jest macierzą hermitowską; f.h. można definiować ogólniej, zastępując ciało  pierścieniem spełniającym odpowiednie warunki i zakładając, że X jest modułem nad tym pierścieniem; w takiej wersji f.h. badał 1853 Ch. Hermite, w związku z pewnymi problemami teorii liczb.
pierścieniem spełniającym odpowiednie warunki i zakładając, że X jest modułem nad tym pierścieniem; w takiej wersji f.h. badał 1853 Ch. Hermite, w związku z pewnymi problemami teorii liczb.