nierówność Höldera,
mat. nierówność prawdziwa dla skończonych ciągów liczb rzeczywistych lub zespolonych |a1b1 + ... +anbn| ≤ (|a1|p + ... + |an|p)1/p(|b1|q + ... + |bn|q)1/q, gdzie p > 1 i 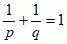 ;
;
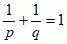 ;
;
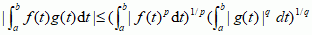 , gdzie p i q spełniają warunki jw., a f i g są funkcjami mierzalnymi na przedziale skończonym lub nieskończonym o końcach a i b (zakłada się, że obie całki po prawej stronie są skończone); nierówność podał L.O. Hölder (1889). Dla p = q = 2 nierówności analogiczne do n.H., tylko z nieskończonymi sumami i całkami, nazywa się odpowiednio nierównością Cauchy’ego–Schwarza i nierównością Buniakowskiego–Schwarza.
, gdzie p i q spełniają warunki jw., a f i g są funkcjami mierzalnymi na przedziale skończonym lub nieskończonym o końcach a i b (zakłada się, że obie całki po prawej stronie są skończone); nierówność podał L.O. Hölder (1889). Dla p = q = 2 nierówności analogiczne do n.H., tylko z nieskończonymi sumami i całkami, nazywa się odpowiednio nierównością Cauchy’ego–Schwarza i nierównością Buniakowskiego–Schwarza.