rozdzielania zmiennych metoda,
mat. sposób znajdowania konkretnych rozwiązań (całkowania) równań różniczkowych: (a) zwyczajnych i (b) cząstkowych;
rozdzielania zmiennych metoda
Encyklopedia PWN
(a) równanie różniczkowe zwyczajne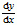 
=
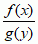, gdzie f, g są funkcjami ciągłymi jednej zmiennej (g(y)≠0) mającymi funkcje pierwotne F, G, uzupełnione warunkiem początkowym y(x0) = y0, ma rozwiązanie y(x) = G–1(F(x)), przy czym F, G należy dobrać tak, aby F(x0) = G(y0) (co, czysto formalnie, odpowiada zapisaniu równania w postaci g(y)dy = f(x)dx, obliczeniu całek nieoznaczonych obu stron i odpowiedniemu dobraniu stałej); (b) niektóre (czasem wszystkie) rozwiązania wielu równań różniczkowych cząstkowych można wyznaczyć, znajdując najpierw rozwiązania jakiejś szczególnie prostej postaci (będące np. sumami bądź iloczynami funkcji jednej zmiennej); np. jednowymiarowe równanie przewodnictwa cieplnego 
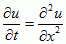, gdzie t > 0, x ∈ [0, π], uzupełnione warunkami u(0, t) = u(π, t) = 0, u(x, 0) = f(x) = 
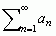sin nx, ma rozwiązanie u(x, t) = 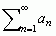exp(−n2t)sin nx, o czym można przekonać się, wyznaczając najpierw wszystkie funkcje u(x, t) = vn(x)wn(t), takie że 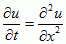, co sprowadza się do scałkowania 2 równań różniczkowych zwyczajnych.
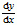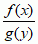=, gdzie f, g są funkcjami ciągłymi jednej zmiennej (g(y)≠0) mającymi funkcje pierwotne F, G, uzupełnione warunkiem początkowym y(x0) = y0, ma rozwiązanie y(x) = G–1(F(x)), przy czym F, G należy dobrać tak, aby F(x0) = G(y0) (co, czysto formalnie, odpowiada zapisaniu równania w postaci g(y)dy = f(x)dx, obliczeniu całek nieoznaczonych obu stron i odpowiedniemu dobraniu stałej); (b) niektóre (czasem wszystkie) rozwiązania wielu równań różniczkowych cząstkowych można wyznaczyć, znajdując najpierw rozwiązania jakiejś szczególnie prostej postaci (będące np. sumami bądź iloczynami funkcji jednej zmiennej); np. jednowymiarowe równanie przewodnictwa cieplnego 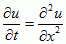, gdzie t > 0, x ∈ [0, π], uzupełnione warunkami u(0, t) = u(π, t) = 0, u(x, 0) = f(x) = 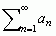sin nx, ma rozwiązanie u(x, t) = 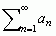exp(−n2t)sin nx, o czym można przekonać się, wyznaczając najpierw wszystkie funkcje u(x, t) = vn(x)wn(t), takie że 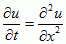, co sprowadza się do scałkowania 2 równań różniczkowych zwyczajnych. 
