równania różniczkowe cząstkowe,
równania zawierające niewiadomą funkcję wielu zmiennych, jej pochodne cząstkowe różnych rzędów i zmienne niezależne;
równania różniczkowe cząstkowe
Encyklopedia PWN
rzędem różniczkowych równań cząstkowych nazywa się największy rząd pochodnej wchodzącej w skład równania, np.
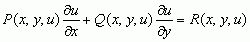 , gdzie funkcje P, Q, R są znane, jest rzędu pierwszego (niewiadomą funkcją jest funkcja u = u(x, y)); jest ono równaniem liniowym, gdyż pochodne ∂u/∂x i ∂u/∂y występują tylko w pierwszej potędze; różniczkowe równanie cząstkowe
, gdzie funkcje P, Q, R są znane, jest rzędu pierwszego (niewiadomą funkcją jest funkcja u = u(x, y)); jest ono równaniem liniowym, gdyż pochodne ∂u/∂x i ∂u/∂y występują tylko w pierwszej potędze; różniczkowe równanie cząstkowe 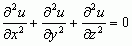 jest liniowe i rzędu drugiego, równanie zaś
jest liniowe i rzędu drugiego, równanie zaś 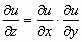 jest nieliniowe i rzędu pierwszego; każdą funkcję, która spełnia dane różniczkowego równania cząstkowego, nazywa się całką tego równania; różniczkowe równania cząstkowe mają na ogół nieskończenie wiele rozwiązań (całek), przy czym rodzina wszystkich całek może zależeć od dowolnej (lub dowolnych) funkcji (a nie od pewnego zespołu dowolnych parametrów liczbowych, czyli tzw. stałych całkowania, jak to ma miejsce w przypadku równań różniczkowych zwyczajnych); np. całka ogólna różniczkowego równania cząstkowego
jest nieliniowe i rzędu pierwszego; każdą funkcję, która spełnia dane różniczkowego równania cząstkowego, nazywa się całką tego równania; różniczkowe równania cząstkowe mają na ogół nieskończenie wiele rozwiązań (całek), przy czym rodzina wszystkich całek może zależeć od dowolnej (lub dowolnych) funkcji (a nie od pewnego zespołu dowolnych parametrów liczbowych, czyli tzw. stałych całkowania, jak to ma miejsce w przypadku równań różniczkowych zwyczajnych); np. całka ogólna różniczkowego równania cząstkowego 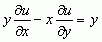 jest postaci u = φ(x2 + y2) + x, gdzie φ jest dowolną funkcją różniczkowalną; analogicznie, rozwiązanie ogólne różniczkowego równania cząstkowego
jest postaci u = φ(x2 + y2) + x, gdzie φ jest dowolną funkcją różniczkowalną; analogicznie, rozwiązanie ogólne różniczkowego równania cząstkowego 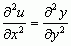 ma postać u = φ (x + y) + ψ (x – y); aby więc wybrać konkretne rozwiązanie jakiegoś różniczkowego równania cząstkowego, należy podać pewne dodatkowe warunki, jakie to rozwiązanie musi spełniać — są to najczęściej tzw. warunki początkowe lub warunki brzegowe; szczególnie duże znaczenie w zastosowaniach mają różniczkowe równania cząstkowe drugiego rzędu.
ma postać u = φ (x + y) + ψ (x – y); aby więc wybrać konkretne rozwiązanie jakiegoś różniczkowego równania cząstkowego, należy podać pewne dodatkowe warunki, jakie to rozwiązanie musi spełniać — są to najczęściej tzw. warunki początkowe lub warunki brzegowe; szczególnie duże znaczenie w zastosowaniach mają różniczkowe równania cząstkowe drugiego rzędu.
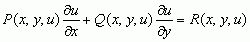 , gdzie funkcje P, Q, R są znane, jest rzędu pierwszego (niewiadomą funkcją jest funkcja u = u(x, y)); jest ono równaniem liniowym, gdyż pochodne ∂u/∂x i ∂u/∂y występują tylko w pierwszej potędze; różniczkowe równanie cząstkowe
, gdzie funkcje P, Q, R są znane, jest rzędu pierwszego (niewiadomą funkcją jest funkcja u = u(x, y)); jest ono równaniem liniowym, gdyż pochodne ∂u/∂x i ∂u/∂y występują tylko w pierwszej potędze; różniczkowe równanie cząstkowe 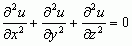 jest liniowe i rzędu drugiego, równanie zaś
jest liniowe i rzędu drugiego, równanie zaś 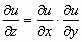 jest nieliniowe i rzędu pierwszego; każdą funkcję, która spełnia dane różniczkowego równania cząstkowego, nazywa się całką tego równania; różniczkowe równania cząstkowe mają na ogół nieskończenie wiele rozwiązań (całek), przy czym rodzina wszystkich całek może zależeć od dowolnej (lub dowolnych) funkcji (a nie od pewnego zespołu dowolnych parametrów liczbowych, czyli tzw. stałych całkowania, jak to ma miejsce w przypadku równań różniczkowych zwyczajnych); np. całka ogólna różniczkowego równania cząstkowego
jest nieliniowe i rzędu pierwszego; każdą funkcję, która spełnia dane różniczkowego równania cząstkowego, nazywa się całką tego równania; różniczkowe równania cząstkowe mają na ogół nieskończenie wiele rozwiązań (całek), przy czym rodzina wszystkich całek może zależeć od dowolnej (lub dowolnych) funkcji (a nie od pewnego zespołu dowolnych parametrów liczbowych, czyli tzw. stałych całkowania, jak to ma miejsce w przypadku równań różniczkowych zwyczajnych); np. całka ogólna różniczkowego równania cząstkowego 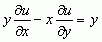 jest postaci u = φ(x2 + y2) + x, gdzie φ jest dowolną funkcją różniczkowalną; analogicznie, rozwiązanie ogólne różniczkowego równania cząstkowego
jest postaci u = φ(x2 + y2) + x, gdzie φ jest dowolną funkcją różniczkowalną; analogicznie, rozwiązanie ogólne różniczkowego równania cząstkowego 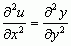 ma postać u = φ (x + y) + ψ (x – y); aby więc wybrać konkretne rozwiązanie jakiegoś różniczkowego równania cząstkowego, należy podać pewne dodatkowe warunki, jakie to rozwiązanie musi spełniać — są to najczęściej tzw. warunki początkowe lub warunki brzegowe; szczególnie duże znaczenie w zastosowaniach mają różniczkowe równania cząstkowe drugiego rzędu.
ma postać u = φ (x + y) + ψ (x – y); aby więc wybrać konkretne rozwiązanie jakiegoś różniczkowego równania cząstkowego, należy podać pewne dodatkowe warunki, jakie to rozwiązanie musi spełniać — są to najczęściej tzw. warunki początkowe lub warunki brzegowe; szczególnie duże znaczenie w zastosowaniach mają różniczkowe równania cząstkowe drugiego rzędu. Teoria i zastosowania równań tego typu oraz niektórych typów równań całkowych i całkowo-różniczkowych są przedmiotem badań wydzielonej dyscypliny mat., zw. teorią równań fizyki mat.; wielkości występujące w tych równaniach mają na ogół bezpośredni sens fiz.; równania fizyki mat. wyprowadza się na podstawie praw i procesów fiz., w mniejszym lub większym stopniu idealizując skomplikowaną zazwyczaj realną sytuację fiz. (np. równanie drgań pręta wyprowadza się na podstawie prawa Hooke’a, pomijając budowę cząsteczkową tego pręta); duże znaczenie w zastosowaniach mają również układy różniczkowych równań cząstkowych, np. układ równań Maxwella, układ równań hydrodynamiki, czy też układ równań Cauchy’ego–Riemanna. Pierwsze równania fizyki mat. pojawiły się w poł. XVIII w. w związku z badaniami procesów drgań rozmaitych środowisk (strun, prętów, membran), jak również w związku z badaniami rozmaitych zagadnień z zakresu akustyki i hydrodynamiki.


