de L’Hospitala reguła

de L’Hospitala reguła,

mat. twierdzenie ułatwiające obliczanie granic wyrażeń nieoznaczonych postaci 0/0 lub ∞/∞: jeśli f i g są funkcjami różniczkowalnymi na pewnym przedziale (a, b) ⊂ ℝ, x₀ jest punktem skupienia tego przedziału i 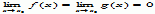lub 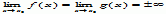, a ponadto granica 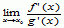istnieje i jest równa A, to granica 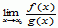też istnieje i jest równa A;

np. aby obliczyć

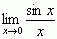lub 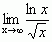, znajduje się oddzielnie pochodne funkcji stojących w liczniku i mianowniku, a następnie — granice ilorazu pochodnych, np.:

,

.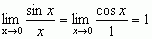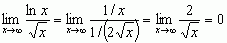