całka powierzchniowa,
mat. całka z funkcji ciągłej f(P) określonej na pewnej powierzchni dwuwymiarowej S, gładkiej, zawartej w ℝ3
całka powierzchniowa
Encyklopedia PWN
całkę powierzchniową oznacza się symbolem 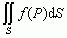 i określa wzorem:
i określa wzorem:
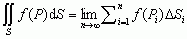 , gdzie △Si — pole elementu powierzchni Si, na które jest podzielona powierzchnia S, Pi — dowolnie wybrany punkt wewnątrz Si; jeżeli powierzchnia S jest zadana parametrycznie: x = x(u, v), y = y(u, v), z = z(u, v), to
, gdzie △Si — pole elementu powierzchni Si, na które jest podzielona powierzchnia S, Pi — dowolnie wybrany punkt wewnątrz Si; jeżeli powierzchnia S jest zadana parametrycznie: x = x(u, v), y = y(u, v), z = z(u, v), to
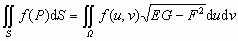 , gdzie E(u, v) = xu2+yu2+zu2, G(u, v) = xv2 + yv2 + zv2, F(u, v) = xuxv + yuyv + zuzv (xu = ∂x/∂u itd.) są współczynnikami pierwszej formy kwadratowej powierzchni, Ω — obszar zmienności parametrów u i v; w przypadku, gdy powierzchnia jest zadana równaniem jawnym z = z(x, y), całka powierzchniowa ma postać:
, gdzie E(u, v) = xu2+yu2+zu2, G(u, v) = xv2 + yv2 + zv2, F(u, v) = xuxv + yuyv + zuzv (xu = ∂x/∂u itd.) są współczynnikami pierwszej formy kwadratowej powierzchni, Ω — obszar zmienności parametrów u i v; w przypadku, gdy powierzchnia jest zadana równaniem jawnym z = z(x, y), całka powierzchniowa ma postać:
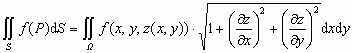 (Ω — obszar zmienności zmiennych x, y); przytoczona definicja jest definicją całki powierzchniowej niezorientowanej; rozważa się też całki powierzchniowe zorientowane;
(Ω — obszar zmienności zmiennych x, y); przytoczona definicja jest definicją całki powierzchniowej niezorientowanej; rozważa się też całki powierzchniowe zorientowane;
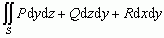 , gdzie np.
, gdzie np. 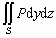 definiuje się jako
definiuje się jako 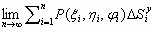 , gdzie
, gdzie 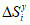 , oznacza pole rzutu na płaszczyznę yz elementu powierzchni Si, przy czym rzut ten zaopatruje się znakiem + lub – w zależności od zwrotu normalnej do danej powierzchni S, a ξi, ηi, φi, oznaczają współrz. dowolnie wybranego punktu w elemencie Si; pozostałe 2 całki
, oznacza pole rzutu na płaszczyznę yz elementu powierzchni Si, przy czym rzut ten zaopatruje się znakiem + lub – w zależności od zwrotu normalnej do danej powierzchni S, a ξi, ηi, φi, oznaczają współrz. dowolnie wybranego punktu w elemencie Si; pozostałe 2 całki 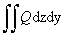 i
i 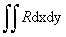 definiuje się analogicznie; wartość pełnej całki powierzchniowej zorientowanej zależy od orientacji powierzchni S. Dla funkcji niekoniecznie ciągłych lub powierzchni niegładkich, definicja całki powierzchniowej jest mniej poglądowa.
definiuje się analogicznie; wartość pełnej całki powierzchniowej zorientowanej zależy od orientacji powierzchni S. Dla funkcji niekoniecznie ciągłych lub powierzchni niegładkich, definicja całki powierzchniowej jest mniej poglądowa.
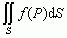 i określa wzorem:
i określa wzorem: 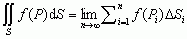 , gdzie △Si — pole elementu powierzchni Si, na które jest podzielona powierzchnia S, Pi — dowolnie wybrany punkt wewnątrz Si; jeżeli powierzchnia S jest zadana parametrycznie: x = x(u, v), y = y(u, v), z = z(u, v), to
, gdzie △Si — pole elementu powierzchni Si, na które jest podzielona powierzchnia S, Pi — dowolnie wybrany punkt wewnątrz Si; jeżeli powierzchnia S jest zadana parametrycznie: x = x(u, v), y = y(u, v), z = z(u, v), to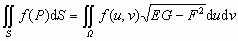 , gdzie E(u, v) = xu2+yu2+zu2, G(u, v) = xv2 + yv2 + zv2, F(u, v) = xuxv + yuyv + zuzv (xu = ∂x/∂u itd.) są współczynnikami pierwszej formy kwadratowej powierzchni, Ω — obszar zmienności parametrów u i v; w przypadku, gdy powierzchnia jest zadana równaniem jawnym z = z(x, y), całka powierzchniowa ma postać:
, gdzie E(u, v) = xu2+yu2+zu2, G(u, v) = xv2 + yv2 + zv2, F(u, v) = xuxv + yuyv + zuzv (xu = ∂x/∂u itd.) są współczynnikami pierwszej formy kwadratowej powierzchni, Ω — obszar zmienności parametrów u i v; w przypadku, gdy powierzchnia jest zadana równaniem jawnym z = z(x, y), całka powierzchniowa ma postać: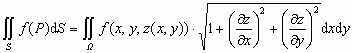 (Ω — obszar zmienności zmiennych x, y); przytoczona definicja jest definicją całki powierzchniowej niezorientowanej; rozważa się też całki powierzchniowe zorientowane;
(Ω — obszar zmienności zmiennych x, y); przytoczona definicja jest definicją całki powierzchniowej niezorientowanej; rozważa się też całki powierzchniowe zorientowane;są to całki postaci
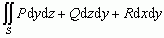 , gdzie np.
, gdzie np. 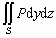 definiuje się jako
definiuje się jako 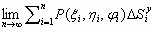 , gdzie
, gdzie 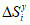 , oznacza pole rzutu na płaszczyznę yz elementu powierzchni Si, przy czym rzut ten zaopatruje się znakiem + lub – w zależności od zwrotu normalnej do danej powierzchni S, a ξi, ηi, φi, oznaczają współrz. dowolnie wybranego punktu w elemencie Si; pozostałe 2 całki
, oznacza pole rzutu na płaszczyznę yz elementu powierzchni Si, przy czym rzut ten zaopatruje się znakiem + lub – w zależności od zwrotu normalnej do danej powierzchni S, a ξi, ηi, φi, oznaczają współrz. dowolnie wybranego punktu w elemencie Si; pozostałe 2 całki 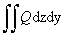 i
i 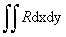 definiuje się analogicznie; wartość pełnej całki powierzchniowej zorientowanej zależy od orientacji powierzchni S. Dla funkcji niekoniecznie ciągłych lub powierzchni niegładkich, definicja całki powierzchniowej jest mniej poglądowa.
definiuje się analogicznie; wartość pełnej całki powierzchniowej zorientowanej zależy od orientacji powierzchni S. Dla funkcji niekoniecznie ciągłych lub powierzchni niegładkich, definicja całki powierzchniowej jest mniej poglądowa. 

