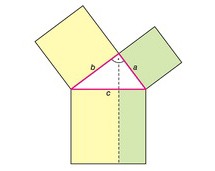
Pitagorasa twierdzenie

Pitagorasa twierdzenie,

mat. pole kwadratu zbudowanego na przeciwprostokątnej trójkąta prostokątnego jest równe sumie pól kwadratów zbudowanych na przyprostokątnych;

jeśli a i b oznaczają odpowiednio przyprostokątne, a c — przeciwprostokątną, wówczas c² = a² + b². Twierdzenie Pitagorasa jest prawdziwe dla figur innych niż kwadraty (figury podobne zbudowane na bokach trójkąta prostokątnego). Równoważne ujęcie twierdzenia Pitagorasa mówi, że trójkąt prostokątny można podzielić na 2 trójkąty podobne do niego (a tym samym na każdą skończoną ich liczbę) — własność ta przysługuje tylko trójkątom prostokątnym. Uogólnieniem twierdzenia Pitagorasa dla dowolnego trójkąta jest tzw. wzór Carnota (cosinusów twierdzenie). Twierdzenie Pitagorasa jest starsze od wszelkich pisanych źródeł z dziejów matematyki.

Twierdzenie Pitagorasa. Pole powierzchni kwadratu c równa się sumie pól kwadratów a i b