funkcje hiperboliczne,
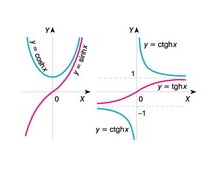
mat. funkcje należące do rodziny funkcji elementarnych: sinus hiperboliczny, cosinus hiperboliczny oraz tangens i cotangens hiperboliczne, określone wzorami:
funkcje hiperboliczne
Encyklopedia PWN
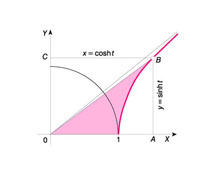
sinh z = 1/2(ez – e–z), cosh z = 1/2(ez + e–z), tgh z = sinh z / cosh z, ctgh z = cosh z / sinh z; wzory mają sens zarówno dla rzeczywistych, jak i zespolonych wartości z; między funkcjami hiperbolicznymi i funkcjami trygonometrycznymi zachodzą związki: sin z = – i sinh iz, cos z = cosh iz (i = 
); funkcje hiperboliczne spełniają m.in. następujące relacje: cosh2 z – sinh2 z = 1 (tzw. jedynka hiperboliczna), (sinh z)′ = cosh z, (cosh z)′ = sinh z; funkcje hiperboliczne odgrywają ważną rolę w geometrii Łobaczewskiego (hiperbolicznej).
); funkcje hiperboliczne spełniają m.in. następujące relacje: cosh2 z – sinh2 z = 1 (tzw. jedynka hiperboliczna), (sinh z)′ = cosh z, (cosh z)′ = sinh z; funkcje hiperboliczne odgrywają ważną rolę w geometrii Łobaczewskiego (hiperbolicznej). 
