Układ aksjomatów geometrii podany przez D. Hilberta (jeden z wielu układów) składa się z 20 aksjomatów podzielonych na 5 grup. Piąta grupa zawiera jedyny aksjomat, który odróżnia geometrię euklidesową od geometrii Łobaczewskiego (
Euklidesa postulat równoległości). Zespół wniosków pochodzących z pierwszych czterech grup aksjomatów Hilberta nosi nazwę
geometrii absolutnej; twierdzenia jej są prawdziwe zarówno w geometrii euklidesowej, jak i w geometrii Łobaczewskiego. W 2. połowie XIX w. na gruncie metody współrzędnych rozwinęły się tzw.
geometrie wielowymiarowe, m.in. takie, w których elementami podstawowymi są nie punkty, lecz proste (J. Plücker) lub kule (S. Lie). Szczególne miejsce zajmuje tu czterowymiarowa geometria Minkowskiego, mająca pierwszorzędne znaczenie w szczególnej teorii względności A. Einsteina. W 1872 F. Klein wystąpił z propozycją pewnej klasyfikacji geometrii (
erlangeński program), która z jednolitego punktu widzenia rozpatrywała różne geometrie: rzutową, afiniczną, euklidesową, nieeuklidesowe i in. Z tego punktu widzenia za geometrię można uważać także topologię, w której są badane najogólniejsze własności przestrzeni. Inny kierunek rozwoju geometrii wiąże się z geometrią różniczkową. Opierając się na badaniach C.F. Gaussa, dotyczących geometrii wewnętrznej powierzchni, Riemann zapoczątkował (1854) nowy dział geometrii —
geometrię przestrzeni riemannowskich. Są to przestrzenie metryczne, tzn. takie, w których jest określona odległość między punktami; wprowadza się tu formę metryczną
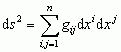
, w której d
s oznacza różniczkę długości łuku krzywej danej za pomocą równań parametrycznych
xi= xi(
t),
i = 1, 2,... ,
n, t — zmienna niezależna, a
gij(x1,... ,
xn) — tzw. tensor metryczny; długość łuku krzywej określa się jako całkę wzdłuż łuku z pierwiastka kwadratowego z formy metrycznej, a odległość 2 punktów jako długość najkrótszego łuku łączącego te punkty, tj. łuku geodezyjnej. Idee Riemanna znacznie przyczyniły się do powstania i rozwoju ogólnej teorii względności. Na przełomie XIX i XX w. na użytek geometrii różniczkowej powstał
rachunek tensorowy, który znalazł szerokie zastosowanie w fizyce i technice, a był i nadal pozostaje niezmiernie wygodnym narzędziem badań geometrii. Nowoczesna geometria różniczkowa zajmuje się m.in. badaniami przestrzeni jako całości, nie zaś małych fragmentów przestrzeni. Ten globalny punkt widzenia zbliża geometrię różniczkową do topologii. Do badań globalnych w geometrii różniczkowej stosuje się obecnie metody topologiczne, zwłaszcza nowo powstałą teorię przestrzeni włóknistych i globalny rachunek wariacyjny zapoczątkowany przez M. Morse’a.
Najbardziej spektakularne osiągnięcia geometrii w ostatnim półwieczu to
teoria katastrof (1958, R. Thom), wyliczająca rodzaje możliwości opisu zjawisk nieciągłych przez zależności ciągłe (liczne zastosowania, np. w medycynie, ekonomii), wykorzystanie geometrii hiperbolicznej do klasyfikacji rozmaitości (1982, W. Thurston) i teoria figur samopodobnych (
fraktal).
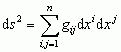 , w której ds oznacza różniczkę długości łuku krzywej danej za pomocą równań parametrycznych xi= xi(t), i = 1, 2,... , n, t — zmienna niezależna, a gij(x1,... , xn) — tzw. tensor metryczny; długość łuku krzywej określa się jako całkę wzdłuż łuku z pierwiastka kwadratowego z formy metrycznej, a odległość 2 punktów jako długość najkrótszego łuku łączącego te punkty, tj. łuku geodezyjnej. Idee Riemanna znacznie przyczyniły się do powstania i rozwoju ogólnej teorii względności. Na przełomie XIX i XX w. na użytek geometrii różniczkowej powstał rachunek tensorowy, który znalazł szerokie zastosowanie w fizyce i technice, a był i nadal pozostaje niezmiernie wygodnym narzędziem badań geometrii. Nowoczesna geometria różniczkowa zajmuje się m.in. badaniami przestrzeni jako całości, nie zaś małych fragmentów przestrzeni. Ten globalny punkt widzenia zbliża geometrię różniczkową do topologii. Do badań globalnych w geometrii różniczkowej stosuje się obecnie metody topologiczne, zwłaszcza nowo powstałą teorię przestrzeni włóknistych i globalny rachunek wariacyjny zapoczątkowany przez M. Morse’a.
, w której ds oznacza różniczkę długości łuku krzywej danej za pomocą równań parametrycznych xi= xi(t), i = 1, 2,... , n, t — zmienna niezależna, a gij(x1,... , xn) — tzw. tensor metryczny; długość łuku krzywej określa się jako całkę wzdłuż łuku z pierwiastka kwadratowego z formy metrycznej, a odległość 2 punktów jako długość najkrótszego łuku łączącego te punkty, tj. łuku geodezyjnej. Idee Riemanna znacznie przyczyniły się do powstania i rozwoju ogólnej teorii względności. Na przełomie XIX i XX w. na użytek geometrii różniczkowej powstał rachunek tensorowy, który znalazł szerokie zastosowanie w fizyce i technice, a był i nadal pozostaje niezmiernie wygodnym narzędziem badań geometrii. Nowoczesna geometria różniczkowa zajmuje się m.in. badaniami przestrzeni jako całości, nie zaś małych fragmentów przestrzeni. Ten globalny punkt widzenia zbliża geometrię różniczkową do topologii. Do badań globalnych w geometrii różniczkowej stosuje się obecnie metody topologiczne, zwłaszcza nowo powstałą teorię przestrzeni włóknistych i globalny rachunek wariacyjny zapoczątkowany przez M. Morse’a.